History

1900: Hilbert's 23 problems for the next century:

• 2nd Problem: prove the axioms of mathematics are consistent
• 6th problem: axiomize physics (UNSOLVED)
• 10th problem: find an algorithm to determine whether given a polynomial Diophantine equation¹ has an integer solution.

Definition 1   Problem: Relation from input to acceptable output.

10th problem can be written as:

Input:

Diaphantine equation.

Output:

Assignment to variables or no solution. Hilbert thought every problem has an algorithm.

To prove that an algorithm does not exist, first we have to define what is an algorithm.

Assumption: any computation device only has finite many useful states/configurations².(By definition, the computation which can be carried by such a device should be called algorithms?)

Theorem 1   No finite state machine can count. That is, no finite state machine can determine if a String 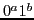$0^a1^b$ has $a = b$.

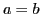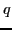
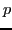
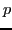
Proof. Consider the state of the machine after reading the inputs. Since it has only finite number of states, there must be two strings end up in the same state, say state $q$. If the first, followed by two 1s, comes to state $p$, then the second must also come to $p$ followed by two 1s.³ $\qedsymbol$

We reject the assumption above, because this doesn't meet our intuition⁴.

Adding more memory to the computer when in need, we get a Turing Machine(TM).