Theorem 8
Cobham Edmonds(Circa 1960): Algorithms that use polynomially bounded resources(time, space)
are generally reasonable for moderately sized inputs.
Algorithms that use exponential resources are essentially always not reasonable for moderately sized inputs.
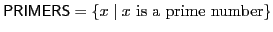 is in
is in
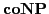 .
.
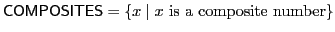 is in
is in
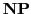 .
.
 16 is in
16 is in
 .
.
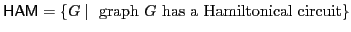 is in
is in
 .17
.17
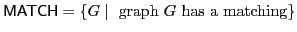 is in
is in
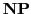 .18
.18
 is in
is in
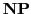 .19
.19
Definition 8
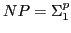 the class of languages
the class of languages 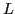 . For which there exists a polynomial time Turing Machine
. For which there exists a polynomial time Turing Machine 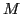 such that
such that
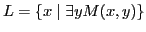 and
and 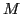 runs in the polynomial time in
runs in the polynomial time in 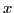 . Here
. Here 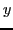 is
of polynomial size in regard of
is
of polynomial size in regard of 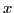 .
.
According to this,
 ,
,
 and
and
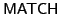 are in
are in
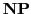 .
.
Definition 9
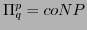 . The class of languages
. The class of languages 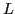 for which there exists
a Turing Machine
for which there exists
a Turing Machine 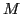 such that
such that
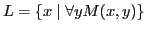 ,
and
,
and 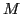 runs in the poly in
runs in the poly in 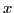 .
.
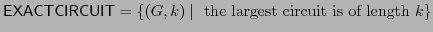 both
both 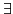 and
and 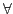 are
used in the first order logic expression. It is in
are
used in the first order logic expression. It is in
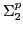
Definition 10
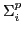 is the class of languages
is the class of languages 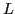 , for which there exists a Turing Machine
, for which there exists a Turing Machine 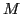 such that
such that
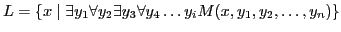 and M runs
in time poly in the size of
and M runs
in time poly in the size of 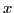 .
.
Definition 11
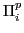 is the class of languages
is the class of languages 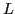 , for which there exists a Turing Machine
, for which there exists a Turing Machine 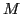 such that
such that
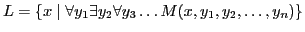 and M runs
in time poly in the size of
and M runs
in time poly in the size of 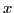 .
.
Definition 12
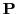 is languages decidable in polynomial time.
is languages decidable in polynomial time.
bighead
2008-10-29
![]() is in
is in
![]() .
.
![]() is in
is in
![]() .
.
![]() 16 is in
16 is in
![]() .
.
![]() is in
is in
![]() .17
.17
![]() is in
is in
![]() .18
.18
![]() is in
is in
![]() .19
.19
![]() ,
,
![]() and
and
![]() are in
are in
![]() .
.
![]() both
both ![]() and
and ![]() are
used in the first order logic expression. It is in
are
used in the first order logic expression. It is in
![]()