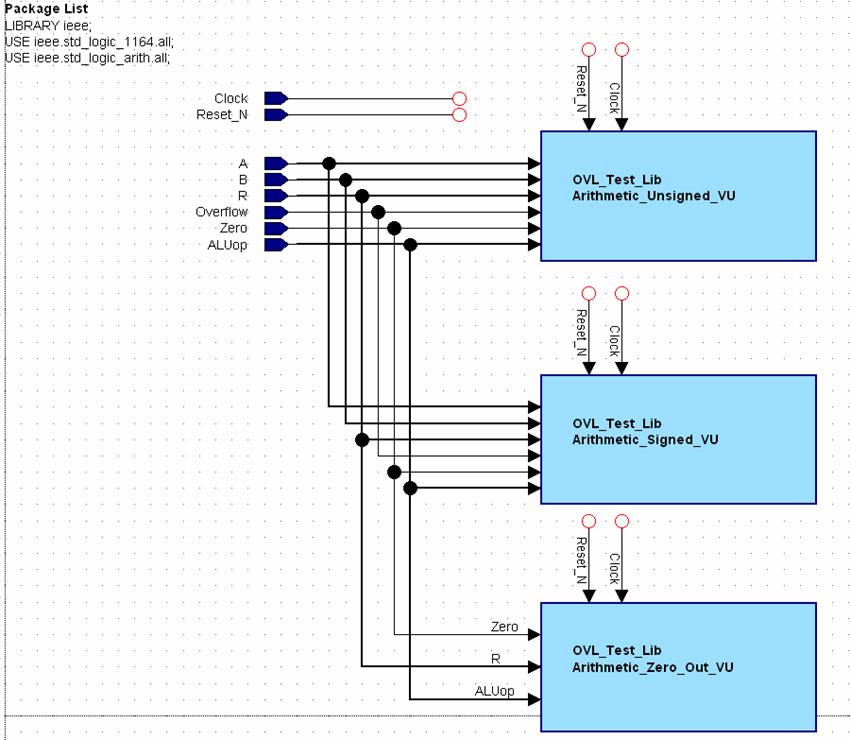
Verification of Arithmetic Operations
Verification of
arithmetic operations are the most difficult
assertions to define, partly because we also have to worry about Overflow. As shown in figure 11, the Arithmetic
verification unit is again divided into signed and unsigned entities. There is also a third entity required to
verify the operation of the ZERO flag.
Figure 11.
Below are the
assertions for Signed additions and subtractions (Don’t forget to add the
correct Package!!!).
The Assertions for the unsigned operations are identical, except for the
Package List definitions and ALU opcodes.
As a side note,
notice that this time instead explicitly assigning output expression true or
false values, we can just assign it the result of the Boolean operation. This makes the code more compact.
--Antecedent
Expression for Signed Addition
antecedent_expr <= (ALUop="0100");
consequent_expr <= ((A + B)=
R);
--Antecedent Expression for Signed Subtraction
antecedent_expr1 <= (ALUop="0110");
consequent_expr1 <= ((A -B)= R);
We know that Overflow has occurred if the result of
the addition of our two operands is larger than the largest possible positive
64-bit number. Likewise, there is
Overflow if the result of our subtraction operation is more negative than the
smallest possible signed 64-bit number.
We can determine if this has occurred by calculating the result and
storing it into a temporary 65-bit variable.
--Antecedent Expression for Signed Addition Overflow
PROCESS (A, B)
VARIABLE R_temp: std_logic_vector(64 DOWNTO 0);
BEGIN
R_temp :=
(A(63)&A)+(B(63)&B); --Operands
also need to be sign extended to 65 bits
if (R_temp >
X"07FFF_FFFF_FFFF_FFFF") AND (ALUop="0100")
then
antecedent_expr3 <= true;
else
antecedent_expr3 <= false;
end if;
END
PROCESS;
--Consequent Expression for Signed Addition Overflow
consequent_expr3 <= (Overflow ='1');
--Antecedent Expression for Signed Subtraction Overflow
PROCESS (A, B)
VARIABLE R_temp: std_logic_vector(64
DOWNTO 0);
BEGIN
R_temp :=
(A(63)&A)-(B(63)&B); --Operands also need to be sign extended to 65
bits
if (R_temp <
'1'&X"8000_0000_0000_0001") AND (ALUop="0110")
then
antecedent_expr4 <= true;
else
antecedent_expr4 <= false;
end if;
END
PROCESS;
--Consequent Expression for Signed Subtraction Overflow
consequent_expr4 <= (Overflow ='1');
Our final assertion is that of the ZERO flag. The ZERO flag should be true when we perform
an ADD/SUB and the result is equal to zero.
--Antecedent Expression for ZERO flag
antecedent_expr <= (ALUop(3 DOWNTO 2) = “01”)
AND (R=X"0000_0000_0000_0000");
--Consequent Expression for ZERO flag
consequent_expr <= (Zero='1');