2.2 CKY Parsing (35 Points)
Author: Yuhuan Jiang
Last updated: Feb 18, 2017
Part I. Non Probabilistic CKY (15 points)
Implement a CKY parser which can parse any given sentence using the provided grammar.
Grammar File
The grammar file cfg.txt (click here to download) provided is exactly the same as the L1 grammar from the textbook.
S -> NP VP
S -> Aux NP VP
S -> VP
NP -> Pronoun
NP -> Proper-Noun
NP -> Det Nominal
Nominal -> Noun
Nominal -> Nominal Noun
Nominal -> Nominal PP
VP -> Verb
VP -> Verb NP
VP -> Verb NP PP
VP -> Verb PP
VP -> VP PP
PP -> Preposition NP
Det -> that | this | a
Noun -> book | flight | meal | money
Verb -> book | include | prefer
Pronoun -> i | she | me
Proper-Noun -> houston | twa
Aux -> does
Preposition -> from | to | on | near | through
Binarization
The grammar provided has rules such as VP -> Verb NP PP,
which has more than two non-terminals on the right hand side. However,
the CKY algorithm can only handle grammars in a binarized format (such
as CNF). Therefore, you need to binarize the grammar before CKY decoding
can be executed. You may use the CNF conversion introduced in class, or
any other binarization techniques.
Using the binarized grammar, the parse tree generated by CKY will not
be in its most natural form (because intermediate non-terminal symbols
introduced by the binarization process may present in the tree). Such
parses are not considered as the final result. You should "debinarize"
(the reverse of binarization) the tree to convert it back to its most
natural form.
Example
Suppose that in your binarization process, the grammar rule VP -> Verb NP PP is broken into VP -> Verb @VP.Verb @VP.Verb -> NP PP. Using this grammar, your CKY produces the following parse tree for some sentence
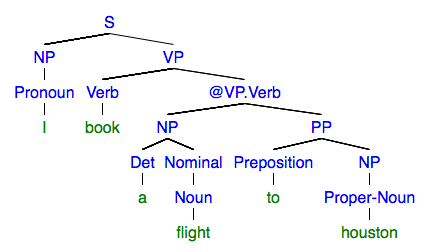
This tree is not in its most natural form because it contains the nonterminal symbol, @VP.Verb, which is not in the original grammar.
You need to post-process this tree to convert it to the following tree
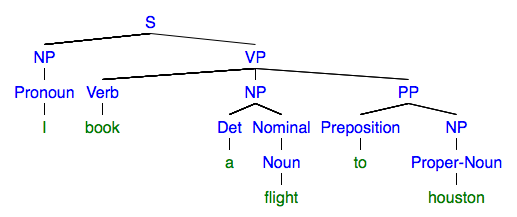
Directly showing the tree containing non-terminals that are not in
the original grammar as the answer without debinarization will result in
point deduction!
Input/Output Requirements
⚠️ Warning
Failing to conform to the the input/output requirement will result in a 5-point deduction.
Your script (for Python users) or executable jar (for Java users) must take two parameters:
- The grammar file
- The sentence to parse (which will be surrounded by double quotes)
For example, when your script cky.py is run as follows,
python cky.py cfg.txt "i book flight"
it should read the grammar in the file cfg.txt, and parse the sentence i book flight using that grammar.
For Java users, the command will be
java -cp yourname.jar cs2731.hw2.CKY cfg.txt "i book flight"
The output should be printed to the standard output stream, and it should answer the following two questions:
- Does the grammar accept the sentence? For this question, you should print a line saying
Sentence accepted! or Sentence rejected!
If accepted, what are the parse trees? For this question, print out each tree using the s-expression, which is a bracket-based format for parse trees. An example:
Example
The tree in the second figure above in s-expression would be
[S [NP [Pronoun I]] [VP [Verb book] [NP [Det a] [Nominal [Noun flight]]] [PP [Preposition to] [NP [Proper-Noun houston]]]]]
(Copy and paste this string into mshang.ca/syntree to visualize it. You will find this tool very useful throughout this homework. )
Part II. Probabilistic CKY (20 points)
Implement a probabilistic CKY parser.
Grammar File
The grammar file pcfg.txt (click here to download) provided is exactly the same as the probabilistic L1 grammar from the textbook.
0.80 S -> NP VP
0.15 S -> Aux NP VP
0.05 S -> VP
0.35 NP -> Pronoun
0.30 NP -> Proper-Noun
0.20 NP -> Det Nominal
0.15 NP -> Nominal
0.75 Nominal -> Noun
0.20 Nominal -> Nominal Noun
0.05 Nominal -> Nominal PP
0.35 VP -> Verb
0.20 VP -> Verb NP
0.10 VP -> Verb NP PP
0.15 VP -> Verb PP
0.05 VP -> Verb NP NP
0.15 VP -> VP PP
1.0 PP -> Preposition NP
Det -> that [0.10] | a [0.30] | the [0.60]
Noun -> book [0.10] | flight [0.30] | meal [0.15] | money [0.05] | flights [0.40] | dinner [0.10]
Verb -> book [0.30] | include [0.30] | prefer [0.40]
Pronoun -> i [0.40] | she [0.05] | me [0.15] | you [0.40]
Proper-Noun -> houston [0.60] | twa [0.40]
Aux -> does [0.60] | can [0.40]
Preposition -> from [0.30] | to [0.30] | on [0.20] | near [0.15] | through [0.05]
Binarization
This is the same as the non-probabilistic case. One extra thing you
should be very careful is that the binarization should be done in a way
that the probability stays the same for equivalent rules before and
after binarization. This will ensure that, for example, the two trees in
the figures above will have the same probability.
Again, remember to convert the trees generated by your probabilistic
CKY algorithm back to its most natural form (no non-terminal that is not
in the original grammar is permitted in the final output).
Input/Output Requirements
If you use Python, your code will be tested as:
python prob-cky.py pcfg.txt "A test sentence ."
If you use Java, your code will be tested as:
java -cp yourname.jar cs2731.hw2.ProbCKY pcfg.txt "A test sentence ."
The output should be printed to the standard output stream. Print the following information
- What is the probability of the sentence? Just print the number.
- What are the parse trees for the sentence? Print each tree in the
s-expression format. Also print the probability of each tree immediately
below the tree.
What to Include in Submission?
For Python users, include:
- The python source files:
cky.py and prob-cky.py.
- A
readme.txt which includes:
- Python version (2 or 3)
- How did you do binarization/debinarization?
- Any known issues that prevent your script from running.
For Java users, include:
- A
yourname.zip archive which includes the Java source.
- A
yourname.jar which is compiled from your source code. The jar should have two main classes, cs2731.hw2.CKY and cs2731.hw2.ProbCKY.
- A
readme.txt which includes:
- How did you do binarization/debinarization?
- Any known issues that prevent your code from running.

