Homework 2 (CS 1671)

Assigned: February 11, 2020

Due: February 27, 2020 (before midnight)

2.1 HMM Decoding (Viterbi) (20 points)

A partial Viterbi calculation is pictured here. This calculation takes us up through t=2 where v2(1) and v2(2) are computed. In the picture, the index 1 is used for the state labeled C and the index 2 is used for the state labeled H. Compute v3(1) and v3(2). You will need the transition and observation probabilities given here.

Think of this as filling in a table where the columns are moments in time and the rows are states in the HMM. Filling in the table with the numbers computed in the diagram above, and adding a column for time t = 0, and showing all the probability cells, it looks like this:

Each cell in the Viterbi table is filled with one of the Viterbi values computed in the diagram. Like the diagram, the table is complete through t=2. The values in the cells represent Viterbi probabilities. The Viterbi probability written as v2(2) represents the probability of the highest probability path that ends at state 2 at time 2.

• (10 points) Submit a completed version of the table above, together with the calculations you used to compute the Viterbi probabilities v3(1) and v3(2).
  • The calculations should show the products producing the path probabilities and the maximization that gives the final Viterbi value.
  • In addition, show how you would do all calculations in log (ln) space as well as directly as products of probabilities (recall Chapter 3).

• (10 points)
  • Report the best path through the HMM that fits the data.
  • Justify your answer by adding back-traces to your table, including the back-traces for column 3. This figure illustrates the idea. The dashed lines represent the best path associated with each Viterbi value. In your submission you can just explain textually how you would modify the figure, e.g., "Add a back-trace link (dashed line) to the back-trace figure going from STATE? at time t = 3 to STATE? at time t = 2."

2.2 CKY Parsing (60 Points)

Implement a non-probabilistic CKY parser.

• (40 points) Demonstrate the correctness of your implementation by running it with the grammar below on the following inputs.
  • The flight includes a meal
  • Book the flight through Houston
  • I book a flight to Houston
  Your implementation should produce all non-probabilistic parsings and print them out in s-expression format.
  Your implementation should also automatically convert the grammar to CNF.
  The last input is also pictured in a following Example below to give you a target parsing to check.
• (20 points) We will also test your implementation on other blind inputs, grammars and sentences. Be sure to consider and test your implementation on any edge cases you can think of.

Grammar File

The sample grammar file cfg.txt (click here to download) provided is exactly the same as the non-probabilistic grammar in Figure 13.1 from the textbook . Your program should read in any grammar file in this .txt format, as we will test it with other grammars besides this one. Also you can assume that letter casing is not problem. So you can lowercase everything or lowercase the first word of the sentence and accept the grammar as is.

Binarization

The grammar provided has rules such as VP -> Verb NP PP, which has more than two non-terminals on the right hand side. However, the CKY algorithm can only handle grammars in a binarized format such as CNF. Therefore, your program will need to binarize the grammar before CKY decoding can be executed. You can't do this manually due to the blind testing of your program. You should use the CNF conversion introduced in class.

Note that when using the binarized grammar, the parse tree generated by CKY will not be in its most natural form (because intermediate non-terminal symbols introduced by the binarization process may be present in the tree). Such parses are not considered as the final result. You should "debinarize" (the reverse of binarization) the tree to convert it back to its most natural form (no non-terminal that is not in the original grammar is permitted in the final output).

Example

Suppose that in your binarization process, the grammar rule VP -> Verb NP PP is broken into
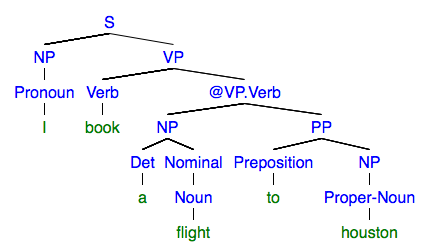
VP -> Verb @VP.Verb
@VP.Verb -> NP PP.
Using this grammar, your CKY produces the following parse tree for some sentence.

This tree is not in its most natural form because it contains the nonterminal symbol, @VP.Verb, which is not in the original grammar. You need to post-process this tree to convert it to the following tree

Directly showing the tree containing non-terminals that are not in the original grammar as the answer without debinarization will result in point deduction!

S-Expression Format

[S [NP [Pronoun I]] [VP [Verb book] [NP [Det a] [Nominal [Noun flight]]] [PP [Preposition to] [NP [Proper-Noun houston]]]]]

(Copy and paste this string into mshang.ca/syntree to visualize it. You will find this tool very useful throughout this homework. )

Input/Output Requirements

⚠️ Warning
Failing to conform to the the input/output requirement will result in a 5-point deduction.

Your script (for Python users) or executable jar (for Java users) must take two parameters:

• The grammar file
• The sentence to parse (which will be surrounded by double quotes)

If you use Python, your code will be tested as:

python cky.py cfg.txt "A test sentence ."

If you use Java, your code will be tested as:

java -cp yourname.jar cs1671.hw2.CKY cfg.txt "A test sentence ."

The output should be printed to the standard output stream. Print the following information

• Does the grammar accept the sentence? For this question, you should print a line saying either "Sentence accepted" or "Sentence rejected". If accepted, you in addition need to print the following.
• What are the parse trees for the sentence? Print each tree in the s-expression format described above.

2.3    Probabilistic Parsing (20 Points)

Take a look at this probabilistic grammar taken from Figure 14.1 of the textbook. Notice that we have productions rules such as VP -> Verb NP PP, which has more than two non-terminals on the right hand side.

• (10 points)
  • Explain how you would modify the algorithm for conversion to CNF to correctly handle rule probabilities.
  • Then show the binarized version of the probabilistic grammar, with the probabilities. You should be very careful that the binarization be done in a way that the probability stays the same for equivalent rules before and after binarization. That is, the CNF should assign the same total probability to each parse tree as the original grammar.

• (10 points) Consider the following PCFG:

  
  1.00  S -> NP VP
  1.00 PP -> P NP  
  0.70 VP -> V NP 
  0.30 VP -> VP PP  
  1.00  P -> with 
  1.00  V -> saw 
  0.40 NP -> NP PP 
  0.10 NP -> scientists 
  0.18 NP -> chins 
  0.04 NP -> saw 
  0.18 NP -> moons 
  0.10 NP -> telescopes 
  

  • What is the probability of the sentence "scientists saw moons with chins"? Show not only the number but its computation.
  • If the sentence is ambiguous, also show the most likely parse using the s-expression format.

What to Include in Submission?

Submit a zip file containing the following pieces:

A writeup for the HMM portion(2.1) of the homework.

A writeup for the Probabilistic Parsing portion(2.3) of the homework.

And the CKY portion described below

For Python users, include:

• The python source file: cky.py.
• A readme.txt which includes:
  • Python version, both major and minor version
  • How did you do binarization?
  • Any known issues that prevent your script from running.

For Java users, include:

• A yourname-cky.zip archive which includes the Java source.
• A yourname-cky.jar which is compiled from your source code. The jar should have a main class named cs1671.hw2.CKY.
• A readme.txt which includes:
  • Java version, both major and minor version
  • How did you do binarization?
  • Any known issues that prevent your code from running.