Trees

Introduction

Key questions for this section:
- What are trees? How are they different from the other data structures seen so far?
- What is the terminology associated with trees?

Almost all of the data structures we have examined so far are all linear. The stack, list, and queue (from assignment 1 ... we'll examine queues in more detail soon) are all organized such that items have a single predecessor and a single successor (except the first and last value). These data structures have worked well so far, but could we benefit from organizing the data differently?

Recall the linked list. Each node had a reference to at most one previous node and at most one next node. What if we allowed nodes to have references to more than one next node? This would give us a tree structure. (Allowing nodes to also have more than one previous node creates graphs, also called networks. They will be a topic covered in CS/COE 1501.)

Example of a simple linked list:

Example of a simple tree:

In this tree example, the red node at the top represents the root of the tree. Trees have only one root node. The root node has no parent (i.e. there is no node in the tree pointing to it).
The blue nodes in the middle are interior nodes. They each have one parent and at least one child.
The grey nodes are leaf nodes. Leaf nodes have no children.

A tree is a non-linear data structure, since we cannot draw a single line through all of the elements (without backtracking through already-visited nodes).

In certain situations, trees are a very useful structure to have. They show up across Computer science. You may see them in Operating Systems (with filesystems), Databases (with storing certain indexes), Artificial Intelligence (with planning, pathfinding, and optimization), and Machine Learning (with Decision Trees). There are many kinds of trees (see Wikipedia for a list of them), but we'll talk just about the basic kind. CS/COE 1501 will introduce you to more and other CS courses will introduce you to some of the relevant ones for those fields.

Some family tree definitions:

Parent - A node is a parent of another node if it directly points to the other node. In the tree above, P is the parent of C.
Child - A node is a child of another node if the other node directly points to it. In the tree above, C is a child of P.
Ancestor - A node is an ancestor of another node if it is the parent of that node, or the parent of the parent of that node (i.e. grandparent), or the parent's parent's parent of that node (i.e. great grandparent), etc. The root is the ancestor of all the other nodes in a tree. In the tree above, A and R are both ancestors of D (but P and C are not ancestors of D).
Descendant - A node is a descendant of another node if it is the child of that node, ot the child of the child of that node (i.e. grandchild), or the child's child's child of that node (i.e. great grandchild), etc. The leaves are all descendants of the root. In the tree above, D is a descendant of A and R.
Siblings - Children of the same parent are called siblings. In the tree above, P, A, X, and Y are all siblings of each other. G and H are siblings of each other, but C is not a sibling with them.

A subtree is a part of a tree that looks like a tree. For any node in the tree (let's call it V), if you only look at V and its descendants, you have a subtree. From V's point of view, it is a tree in itself. For example, these are all subtrees of the tree above:

the subtree rooted at P (i.e P and its descendant C)
the subtree rooted at A (i.e A and its descendants G, H, and D)
the subtree rooted at H (i.e. H and D)
the subtree rooted at X (i.e. X)

Using this idea of subtrees, we can define a tree recursively. T is a tree if:

T is empty (i.e. it has no nodes), or
T is a node with 0 children, or
one or more children that are all trees

Which of those are base cases and which are recursive cases?

Let's take a look at an example on the board.

How do we represent an arbitrary tree?

Binary Trees

Key questions for this section:
- What are binary trees?

In many applications, we can limit the structure of our tree somewhat. One common limitation is to allow nodes to only have 0, 1, or 2 children. This is called a Binary Tree. Just like all other trees, binary trees can be defined recursively. T is a binary tree is:

T is empty, or
T is a node with the following structure:

left child element right child

where "left child" and "right child" are binary trees, and "element" is some data value

An example of a binary tree.

Tree Height

Key question for this section:
- What is the definition of "height" for a tree?

The height of a tree is the maximum number of nodes from the root to any leaf. In the tree above, the height is 6 (R → B → E → H → K → L). Subtrees can also have heights. What do you think the height of the subtree rooted at D is?

Height is an important property for trees. As we will see later, many binary tree algorithms have run-times proportional to the tree height. So, let's establish some bounds on height.

Maximum Height – Given a binary tree with n nodes, what is the maximum value it could have for its height? What would this tree look like? Let's discuss this in class.
Minimum Height – Given a binary tree with n nodes, what is the minimum value it could have for its height? What would this tree look like?

Height of Full and Complete Trees

Key questions for this section:
- What is a full tree? What is a complete tree?
- How do you calculate the height of a full tree? of a complete tree?

To determine the minimum height, we need to consider the branching at each node. A minimum-height tree will have the maximum branching at each node. If the number of nodes is n = 2^k - 1 (for any positive integer k), this will be a Full Tree. The root node and all interior nodes have two children. All leaves are on the same, last level of the tree. For example, the tree below is a full tree of height 3 and it has n = 2³ - 1 = 7 nodes.

So where did that formula come from? Note the number of nodes at each level of a full tree:

Level 1: 1 node = 2⁰
Level 2: 2 nodes = 2¹
Level 3: 4 nodes = 2²
...
Level i: 2^2-i nodes

The total number of nodes in a tree of height h is the sum of the nodes at each level:

n = 2⁰ + 2¹ + 2² + ... + 2^h-1

This is the geometric series:

n = SUM_{{from i = 0 to h-1}} 2ⁱ
n = 2^h - 1

So, with a height h, we know the number of nodes for a full tree is 2^h - 1, but what we're really curious about is the reverse. If we know the number of nodes in a full tree is n, what is the height of the tree? How would you determine that?

The analysis above assumes a full tree. That is, each level (including the bottom) has the maximum number of nodes. That is, the above only works for trees with 2^k-1 nodes (e.g. 1, 3, 7, 15, ...). But, binary trees can have any number of nodes. Will this change the formula? Not significantly. We can say that the minimum height for a tree with n nodes is O(log₂ n).

A complete tree is a full tree up to the second-to-last level with the last level of leaves being filled in from left to right. If the last level is completely filled in, the tree is full. A Complete Binary Tree of height h has between 2^h-1 and 2^h-1 nodes (why?).

A nice property of a complete binary tree is that its data can be efficiently stored in an array or vector. Let's take a look at how on the board. Why do you think this is a nice property? When we talk about Priority Queues, we'll see just how useful this can be.

Calculating the Height of a Tree

Key questions for this section:
- What is the general method for determining the height of a tree?

What if we aren't dealing with a complete tree (or a full tree, which is a special case of complete tree)? What if we aren't dealing with a binary tree? How would we calculate the height of a tree in these cases? One way that will work for all trees is to determine the height recursively:

height(T):
    if T is empty:
        return 0
    else:
        LeftHeight = height(T.left)
        RightHeight = height(T.right)
        return 1 + max(LeftHeight, RightHeight)

Let's use this to determine the height of the binary tree shown below:

Representing a Binary Tree

Key questions for this section:
- How do you efficiently represent a binary tree in a program?

We'd like to be able to do operations on binary trees, such as:

Implement the height that we just discussed
Traverse the tree in various ways
Find other properties, such as:
- Max or min value
- Number of nodes

However, before we can do these we need to find a good way to represent the tree in the computer. We'll do this in an object-oriented way, as we did with our lists. It will get a bit complicated, so be prepared to spend some time understanding it. Let's start with an interface:

public interface TreeInterface<T>
{
    public T getRootData();
    public int getHeight();
    public int getNumberOfNodes();
    public boolean isEmpty();
    public void clear();
}

This is an interface for general trees, not just binary trees. An interface specifically for binary trees could be:

public interface BinaryTreeInterface<T> extends TreeInterface<T>, TreeIteratorInterface<T>
{
public void setTree(T rootData);
public void setTree(T rootData, BinaryTreeInterface<T> leftTree, BinaryTreeInterface<T> rightTree);
}

These methods allows for an "easy" assignment of binary trees. We'll look at TreeIteratorInterface<T> later. Now we have the basic functionality of a binary tree, but we need to get the basic structure. Before we get to that though, why do you think we first created the TreeInterface interface?

Let's take a look at the structure. Recall our linked list data structures. The "building blocks" for our lists were Node objects that we defined in a different class (which we called the Node class). This Node class could be separate from the Linked List class for greater re-use and flexibility. Or, the Node class could be an inner class for access convenience. We will do something similar for our binary trees. We will define a BinaryNode class to represent the inner structure of our tree. This class will be more complex than our Node class because there are more things needed to manipulate our binary tree nodes.

Below is the data and set of methods for the BinaryNode class:

class BinaryNode<T>
{
    private T data;
    private BinaryNode<T> leftChild;
    private BinaryNode<T> rightChild;

    public T getData();
    public void setData(T newData);

    public BinaryNode<T> getLeftChild();
    public BinaryNode<T> getRightChild();

    public void setLeftChild(BinaryNode<T> newLeftChild);
    public void setRightChild(BinaryNode<T> newRightChild);

    public boolean hasLeftChild();
    public boolean hasRightChild();

    public boolean isLeaf();

    public int getNumberOfNodes();

    public int getHeight();

    public BinaryNode<T> copy();
}

Notice that it is self-referential, just like linked list nodes. However, they can now branch in two directions, allowing us to easily define a binary tree. We also have some additional methods to manipulate / access our tree.

Now that our BinaryNode class is described, let's look at what data is needed for the BinaryTree class:

public class BinaryTree<T> implements BinaryTreeInterface<T>
{
private BinaryNode<T> root;
}

It turns out, we can create the binary tree through composition. We can use a reference to a BinaryNode object to fully store our tree. Why is that? How would we manipulate a BinaryTree object?

Implementing Operations

Key questions for this section:
- What are common techniques for operating on trees?

Let's now look at how to implement some of the common tree operations. We'll start with the tree's height. Above, we saw how a tree's height is defined and how to calculate it. How would you translate that pseudocode into Java code that uses our binary tree representation discussed above?

How about copying a tree? Copying an array or linked list is fairly simple due to their linear natures. However, it is not immediately obvious how to copy a binary tree such that the nodes are structurally the same as the original. Luckily, we can make use of recursion to achieve this. To copy a tree, we simply:

Make a new node for the root and copy its data
Recursively copy the left subtree into the left child
Recursively copy the right subtree into the right child

Thanks to the idea of subtrees from above, each recursive call will think it's working with the root of a (sub)tree. Let's look at the code:

public BinaryNode<T> copy()
{
    BinaryNode<T> newRoot = new BinaryNode<T>(data);
    if (leftChild != null)
    {
        newRoot.setLeftChild(leftChild.copy());
    }
    if (rightChild != null)
    {
        newRoot.setRightChild(rightChild.copy());
    }
    return newRoot;
}

Note the similarities (and differences) to the code for getHeight(). Both are essentially traversing the entire tree, processing the nodes as they go. Let's take a look at how this code works by making a copy of this tree:

Tree Traversal

Key questions for this section:
- How do you navigate through a tree?
- When might it matter which traversal you use?

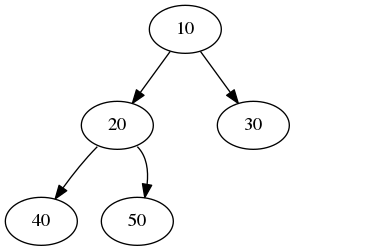
In the two methods above, we saw how to traverse (or walk through) a binary tree. This is a very common operation for trees, as it is with many data structures. For the data structures we've see so far, it was fairly easy to know how to walk through them. They were all linear, so if you start at the beginning, you have only one direction to go. With a tree, if you start at the beginning (the root), you immediately have two choices: go left or go right. Which way do you go? Well, to get to all the data, you need to go both ways. But since you can only go one way at a time, you'll need to start with one then come back to the other. To accomplish this, we can make use of recursion (as we did with the two methods above).

There are three common traversals used for binary trees. They are all similar; the only difference is where the current node is visited relative to the recursive calls.

PreOrder(T):
if (T is not empty)
    Visit T.data
    PreOrder(T.leftChild)
    PreOrder(T.rightChild)
InOrder(T):
if (T is not empty)
    PreOrder(T.leftChild)
    Visit T.data
    PreOrder(T.rightChild)
PostOrder(T):
if (T is not empty)
    PreOrder(T.leftChild)
    PreOrder(T.rightChild)
    Visit T.data

Let's take a look at the order produced by each traversal technique for the following tree:

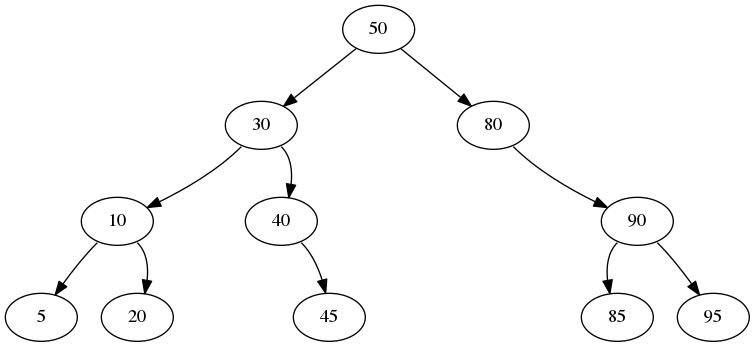
The actual code for these traversals is not any more complicated than the pseudocode. See BinaryNode.java and BinaryTreeExample.java. It uses one tree that is NOT a BST and one that is. Note how the work is done through the recursive calls. The runtime stack "keeps track" of where we are. What do you think the runtimes of these traversals is?

Notice again how the traversals, getHeight(), and copy() are all similar. In fact, all of these methods are traversing the tree. They differ in the order (pre, in, post) and what is done at each node as it is visited. The getHeight() method can be thought of as a post-order traversal, since we have to get the height of both subtrees before we know the height of the root. The copy() is actually a combination of all three orderings: the root node is created pre-order, the left child is assigned in-order, and the right child is assigned post-order.

These traversals can be done iteratively, but now we need to "keep track" of where we are ourselves (how was our position kept track of above?). We do this by using our own stack of references. The idea is that the "top" BinaryNode reference on our stack is the one we are currently accessing. This works but it is much more complicated than the recursive version. The author uses the iterative versions of these traversals to implement iterators of binary trees. However, we can't use the recursive version for an iterator, since it needs to proceed incrementally (as in a while loop). See BinaryTree.java for an example of how to create binary tree iterators.

Binary Search Tree

Key questions for this section:
- What are binary search trees? How do they differ from binary trees?

Binary Trees are nice, but how can we use them effectively as data structures? One way is to organize the data in the tree in a special way, to create a binary search tree (BST). A binary search tree is a binary tree such that, for each node in the tree:

All data in the left subtree of that node is less than the data in that node
All data in the right subtree of that node is greater than the data in that node

Note that this definition does not allow for duplicates. How would we allow for duplicates?

Since binary search trees are just binary trees with an extra constraint, we can also define binary search trees recursively. A binary tree, T, is a BST if:

T is empty, or
T is a node with the following structure:

left child element right child

where:
- "element" is some data value
- all values in the tree rooted at "left child" are less than "element"
- all values in the tree rooted at "right child" are greater than "element"

This is an example of a binary search tree:

This is also an example:

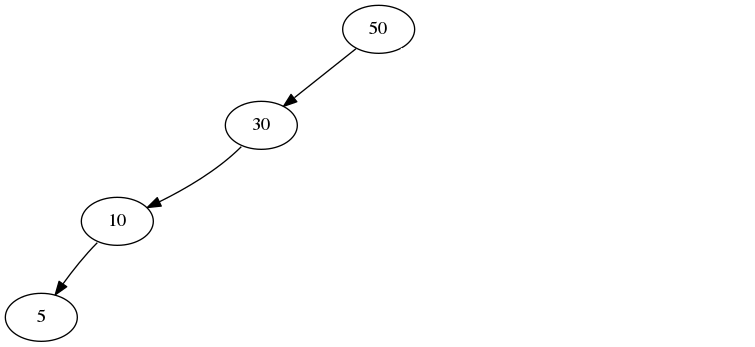
Notice that in both cases, any left branch has values that are less than the node and any right branches has values greater than the node. The tree below is not a binary search tree because this property is violated:

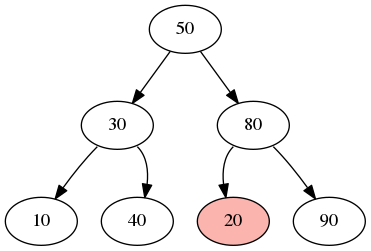
Even though 20 is less than 80 and branches to the left of 80, the entire right branch of the root (50) is not greater than 50. In other words, all of the descendants on the right of 50 must be greater than 50, but they aren't (because of 20 being on the right).

Specification

Key questions for this section:
- What operations does a Binary Search Tree have?
- How does searching a Binary Search Tree compare to a sorted array? to a linked list?

Now that we have a basic understanding of what Binary Search Trees are and their key properties, let's look at how the Binary Search Tree Abstract Data Type is defined. Actually, the book defines a more general type which the Binary Search Tree implements, so we will look at the more general type first.

The Search Tree interface has the following methods:

public boolean contains(T entry)
- Is an entry in the tree or not?
public T getEntry(T entry)
- Find and return an entry that "equals" the parameter entry. If entry is found, return the object, otherwise return null. What is the use of this method?
public T add(T newEntry)
- Add a new entry into the tree. This new object is put into its appropriate location, keeping the search property of the tree intact.
- If an object matching newEntry is already present in the tree, replace it and return the old object. What if we don't want to replace it? Implications?
public T remove(T entry)
- Remove entry from the tree and return it if it exists; otherwise return null
public Iterator<T> getInorderIterator()
- Return an iterator that will allow us to go through the items sequentially from smallest to largest. (See Iterator interface for details)

Before we discuss the implementation details, let's get a feel for the structure by seeing how the getEntry(T entry) method would work. Consider a recursive approach (naturally). What are the questions we must consider when writing a recursive algorithm? How would we answer those questions for this method?

Let's work through an example.

Notice the similarity between this algorithm and one we saw earlier this semester? This is not coincidental! In fact, if we have a full binary tree, and we have the same data in an array, both data structures would search for an item following the exact same steps. Let's look for item 45 in both data structures:

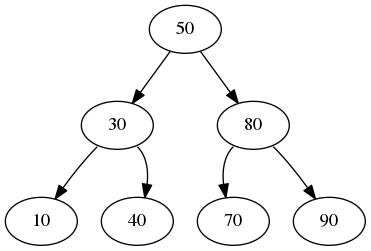
In the case of the array, 45 is "not found" between 40 and 50, since there are no actual items between 40 and 50. In the case of the Binary Search Tree, 45 is "not found" in the right child of 40, since the right child does not exist. Both are base cases of a recursive algorithm. They have the same runtimes since the height of a full tree is O(log₂(n)).

From this example, we can see an advantage of the Binary Search Tree over the LinkedList. Even though both require references to be followed when accessing nodes, the tree structure improves our search time from O(n) to O(log₂(n)). Is the Binary Search Tree an improvement over the array? To answer that question, we need to look at some more operations and their implementations.

Implementation

Key questions for this section:
- For the operations Binary Search Trees support, how are they implemented?
- How do you traverse a tree with the intent to manipulate it?
- How do you traverse a binary search tree iteratively?
- What are the runtimes of the various operations?

We will use the BinaryTree as the basis. We can implement it either recursively or iteratively; we'll look at both versions.

public class BinarySearchTree<T extends Comparable<? super T>> extends BinaryTree<T> implements SearchTreeInterface<T>

We will concentrate on four fundamental operations:

getEntry - Find an object in the tree
add - Add a new object to the tree
remove - Remove an object from the tree
getInorderIterator - Traverse the tree to view all objects

Notice that the contains operation is not included. Why do you think it's not included?

getEntry

We already discussed the idea of this method in a recursive way. Now let's look at the actual code and trace it in both recursive (BinarySearchTree.java) and iterative (BinarySearchTreeI.java) implementations. Note how iterations of the loop correspond to recursive calls.

add

This one is more complicated. There is a special case if the tree is empty, since we need to create a root node. Otherwise, we call addEntry(), which proceeds much like getEntry(). However, we have more to consider. Consider these possibilities at current node (call it temp):

New data is equal to temp.data
- Store old value, assign new value and return old node
New data is less than temp.data
- If temp has a left child, go to it
- Otherwise, add a new node with the new data as the left child of temp
New data is greater than temp.data
- If temp has a right child, go to it
- Otherwise, add a new node with the new data as the right child of temp

Of course, the actual code is trickier than the pseudocode above. Let's trace through the recursive implementation (in BinarySearchTree.java) to see how it works. Let's see how to add 25 to the BST below:

One interesting difference from getEntry/findEntry is that the base case for addEntrymust be at an actual node. We cannot go all the way to a null reference, since we must link the new node to an existing node. If we go to null we have nothing to link the new node to. Thus we stop one call sooner for the base case for addEntry.

This recursive implementation is elegant but it still requires many calls of the method. As we know, this adds overhead to the algorithm. If we do the process iteratively, this overhead largely goes away. So let's take a look at the iterative implementation (in BinarySearchTreeI.java). As with findEntry, since the recursive calls are "either the left child or the right child" but not both, the iteration is very simple and actually preferred over the recursive implementation.

remove

The idea of a remove is simple:

Find the node
Delete it

However, it is much trickier than an add operation. Unlike add, which is always at a leaf, the remove operation could remove an arbitrary node. Depending upon where that node is, this could be a problem. Let's look at 3 cases, and discuss the differences between them.

Node is a leaf
- This one is easy. How would you remove this node from the tree?
Node has one child
- This one is not much harder. In fact, it looks a lot like removing from another data structure we've already seen.
Node has two children
- This one is tricky! The node has only one reference coming in, but two going out. So to actually delete the node would require significant reorganization of the tree. But do we really even need to delete the node? No, we need to delete the data. Perhaps we can accomplish this while leaving the node itself where it is. How?
- Recall that what is important about a BST is the BST Property (i.e. the ordering). The shape is irrelevant (except for efficiency concerns, which we will discuss next). So perhaps we can move data from another node into the node whose value we want to delete. Perhaps the other node will be easier to delete.
- How do we choose this node? Consider an inorder traversal of the tree. We could substitute the value directly before (inorder predecessor) or the value directly after (inorder successor). How do we find this node? Consider inorder predecessor: it is the largest value that is less than the current value. So we go to the left one node, then right as far as we can. What if this node also has two children? It never will, since we know by how we found it that it has no right child (otherwise we would have gone to it).

Let's look at the code to see how this is done. We'll look at the iterative version (in BinarySearchTreeI.java). The recursive version works, but due to the same issues we discussed for add, we will prefer the iterative. Note that the code looks fairly tricky, but in reality we are just going down the tree one time, then changing some references. A lot of the complexity of the code is due to the author's object-oriented focus. Let's see how removal works on the tree shown below.

getInorderIterator

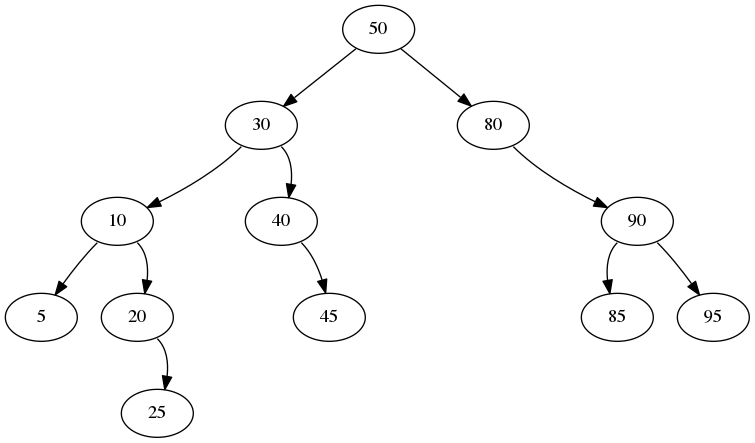
As we discussed previously, this will be a step-by-step inorder traversal of the tree. It is done iteratively so that we can pause indefinitely after each item is returned. Still, the logic is much less clear than for the recursive traversals. This method is implemented in the BinaryTree class, so we don't have to add anything for BinarySearchTree. All we need to do is return an instance of a private InorderIterator object, so we'll focus our attention to that object/class.

Recall the methods we need for an iterator:

hasNext: is there an item left in the iteration?
next: return the next item in the iteration
remove: remove the value returned by the last next method call

We will also need some instance variables. Since iterators must operate iteratively, we cannot make use of the runtime stack to keep track of our location. Instead, we need to mimic the behavior of the runtime stack by using our own Stack object. Another instance variable will be a BinaryNode reference to store the current node.

Let's think now about how the iterator will work. How does inorder traversal work recursively? How can we duplicate that iteratively?

Initially (in the constructor), set the currentNode to the root. For the first call of next():

Go left from currentNode as far as we can, pushing each node onto the stack (including currentNode).
Pop off the top of the stack. This will be nextNode, the next value in the iteration (i.e. the value to be returned).
Set the currentNode to the right child of nextNode. If it has no right child, it is set to null.
Return nextNode's data

On the next call to next():

if currentNode is not null, repeat the steps above
if currentNode is null, repeat the steps above, but start at #2

Let's see an example with this tree:

Runtimes

So how long will getEntry(), contains(), add(), and remove() take to run? It is clear that all of their runtimes are proportional to the height of the tree. So we return to the question of "What are the bounds on the height of a tree with N nodes?".

Normally, trees tend to stay balanced. However, it is possible that the tree is significantly unbalanced if the data is inserted in a particular way. So if the Binary Search Tree is balanced (i.e the average case), they will all be O(log₂(n)). However, if they are very unbalanced (i.e. the worst case), the runtime will be O(n).

So how does a binary search tree compare to a sorted array or ArrayList? Recall that a sorted array gives us (on average):

O(log₂(n)) to find an item using binary search
O(n) to add or remove an item (due to shifting)

Thus, in the average case, binary search trees are better for add and remove, and about the same for find.

So, "on average", a binary search tree will remain balanced. But it is possible for it to become unbalanced, yielding worst case runtimes. Can we guarantee that the tree remains balanced? Yes, for example the AVL Tree (Chapter 27). When adds or removes are done, nodes may be "rotated" to ensure that the tree remains balanced. However, these rotations add overhead to the operations (although runtimes are still O(log(n))). In CS/COE 1501, you will learn about B tree and B+ trees, which also attempt to remain balanced (but are not binary trees).

<< Previous Notes

Daily Schedule

Next Notes >>