Recursion
Introduction
- Key questions for this section:
- What is recursion?
- When should you use it?
The idea behind recursion (and a hint for when to use recursion) is that some problem P is defined/solved in terms of one or more problems P', which are identical in nature to P but smaller in size. To use recursion, the problem must have:
- One or more base cases in which no recursive call is made
- One or more recursive cases in which the algorithm is defined in terms of itself
- The recursive cases must eventually lead to a base case
Simple Examples
- Key questions for this section:
- How do you use recursion to solve a problem?
The examples in this section are designed to help you think about how to apply recursion to a problem. These simple examples are not good examples of when to use recursion, just how to use recursion to solve a problem.
Factorial (N!)
The factorial of a positive integer N is defined as the product of all of the positive integers between 1 and N (inclusive). In other words: N! = N * (N-1) * (N-2) * ... * 1 Additionally, 0! is often defined as 1. Let's look at how to write a recursive implementation:
- N! = N * (N-1)! (when N > 0)
- N! = 1 (when N = 0)
Let's look at our 3 requirements:
- At least one base case:
- N! = 1 when N = 0
- At least one recursive case:
- N! = N * (N-1)! when N > 0
- Recursive case eventually leads to base case
- Since the recursive case has argument of N-1, it should always lead to a base case...but does it always?
Integer Powers (XN)
A number (X) raised to a positive integer (N) is defined as multiplying X by itself (N-1) times. For example, X2 = X * X.
What is a recursive definition of XN? What would be our 3 requirements:
- At least one base case
- At least one recursive case
- Recursive case eventually leads to base case
Writing Recursive Methods
- Key questions for this section:
- How do you translate recursive definitions into methods?
- How does the computer and/or operating system handle recursive functions? How does it work at a low level?
Many recursive methods are very similar to the underlying definitions. Let's look at Factorial:
public long factorial (int N)
{
if (N < 0)
throw new IllegalArgumentException();
if (N <= 1)
return 1;
return N * factorial(N-1);
}
Note that negative N generates an exception. Notice also that the method is calling itself and uses the result in the return expression. Why do you think the return type is long instead of int?
What do you think the integer powers recursive method would look like?
How does recursion work?
Often, students struggle to understand how recursion works. They often wonder how a method is able to call itself and maintain two sets of values for the same local variable. There are two important ideas that allow recursion to work: Activation Record and Run-Time Stack.
An Activation Record is a block of memory allocated to store arguments for method parameters, local variables, and the return address during a method call. An activation record is assocated with each method call, so if a method is called multiple times, multiple records are created. For example, with the factorial method above and this method call:
long result = factorial(3);
The activation record might look like this:

The return address is the set by the operating system. It refers to the next instruction to execute once the method call is finished. In this particular example, the next instruction would probably be something like "save the returned value into the variable result".
The Run-Time Stack is an area of the computer's memory which maintains activation records in Last In First Out (LIFO) order. Recall our previous discussion of Stacks.
When a method is called, an activation record containing the parameters, return address, and local variables is pushed onto the top of the run-time stack. If the method subsequently calls itself, a new, distinct activation record containing new data is pushed onto the top of the run-time stack. The activation record at the top of the run-time stack represents the currently-executing call. Activation records below the top represent previous calls that are waiting to be returned to. When the top call terminates, control returns to the address from the top activation record and then the top activation record is popped from the stack. For example, consider this simple class:
class RecursionExample
{
public static void main(String [] args)
{
int num = 3;
long result;
result = factorial(num);
}
public long factorial (int N)
{
long result;
if (N < 0)
throw new IllegalArgumentException();
if (N <= 1)
return 1;
result = factorial(N-1);
return N * result;
}
}
Here is an illustration of how the recursion, activation records, and run-time stack works:
| Instruction(s) Executed |
Computer Memory After Instructions Executed |
Program starts
In main:
int num = 3;
long result;
|
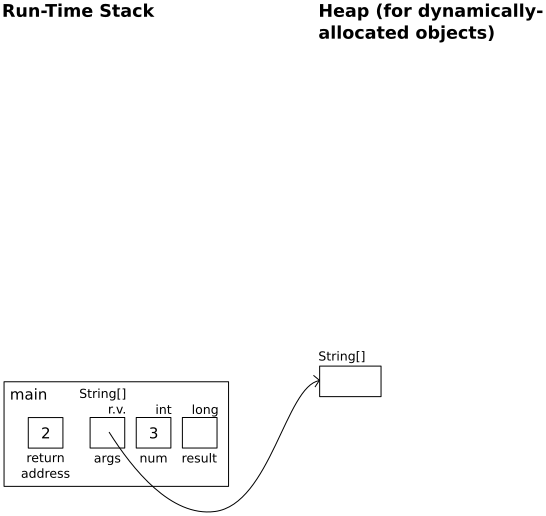
|
In main:
result = factorial(num);
|
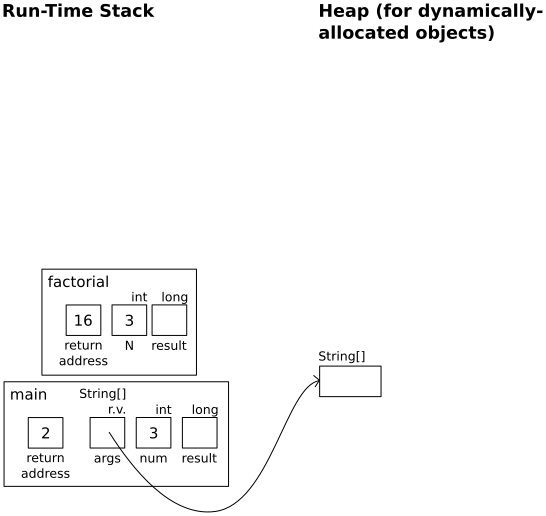
|
In factorial(3):
if (N < 0)
throw new IllegalArgumentException();
if (N <= 1)
return 1;
result = factorial(N-1);
|
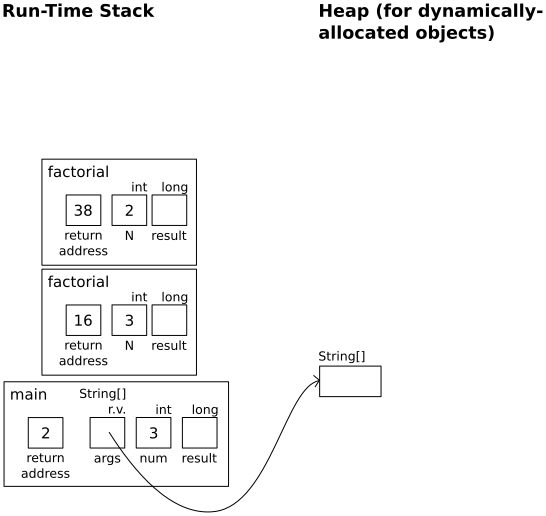
|
In factorial(2):
if (N < 0)
throw new IllegalArgumentException();
if (N <= 1)
return 1;
result = factorial(N-1);
|
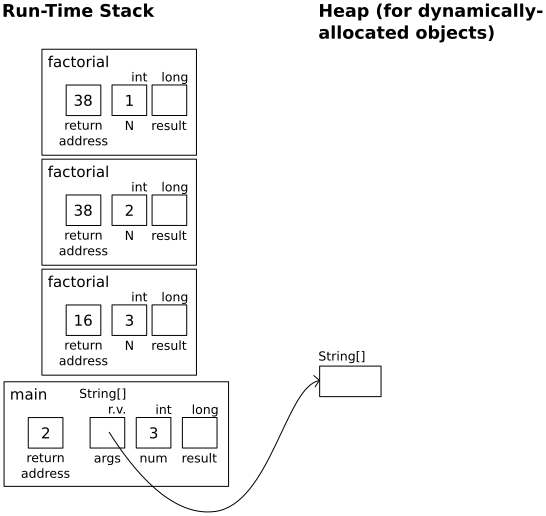
|
In factorial(1):
if (N < 0)
throw new IllegalArgumentException();
if (N <= 1)
|

|
In factorial(1):
if (N <= 1)
return 1;
In factorial(2):
result = factorial(N-1);
|
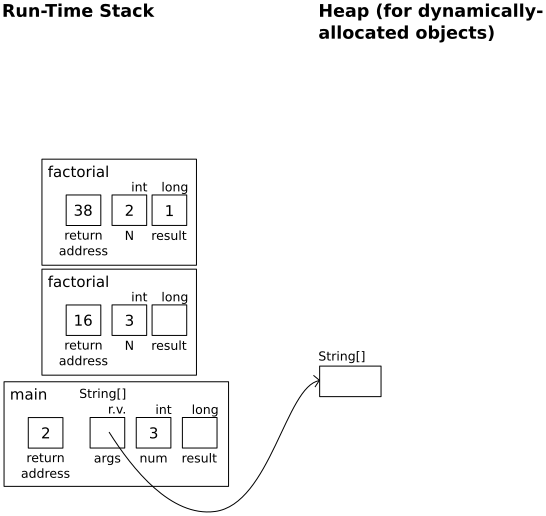
|
In factorial(2):
return N * result;
In factorial(3):
result = factorial(N-1);
|
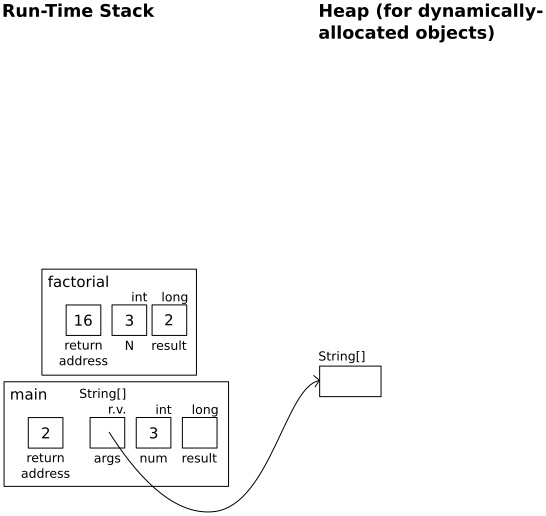
|
In factorial(3):
return N * result;
In main:
result = factorial(num);
|
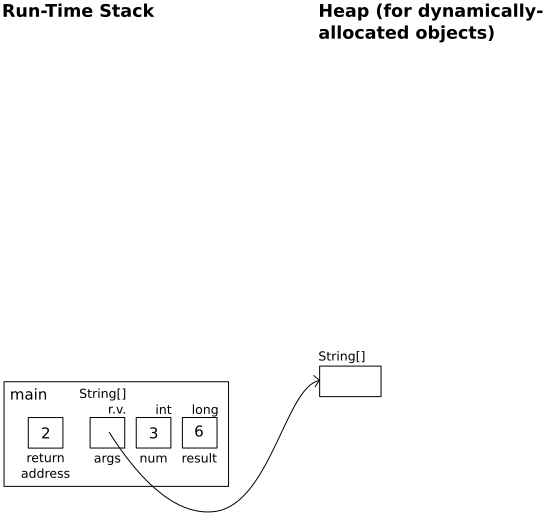
|
A couple of notes about this illustration:
- This is a simplification of what is actually happening. The true explanation is beyond the scope of this course (it's probably explained in CS 447 or CS 449).
- You may be wondering where those return addresses come from. Basically:
- return address 2 corresponds to ending the program
- return address 16 corresponds to the
main method, where the result of the factorial method call is stored into result
- return address 38 corresponds to the
factorial method, where the result of the factorial method call is stored into result
These addresses are made up for the example. There is no way for you to look at the code and know those addresses.
For another example of recursion in action, see RecursionTrace.java.
Recursive Sequential Search
Let's look at one more simple example: Sequential Search, where we find a key in an array or linked list by checking each item in sequence. We know how to do this iteratively (see the bag implementations of contains), it's basically a loop to go through each item. Let's now look at how to do it recursively. Remember, we always need to consider the problem in terms of a smaller problem of the same type. What are:
- Base case
- Recursive case
- Recursive calls must lead to base case
For an implementation of recursive sequential search, see SeqSArray.java.
Let's also consider recursive sequential search of a linked list. What is similar and what is different from the array-based version?
- Base case not found?
- Base case found?
- Recursive case?
- What if list is initially empty?
- What if
list.getNextNode() == null
For an implementation of recursive sequential search with a linked list, see SeqSLinked.java (and Node.java).
Divide and Conquer
- Key questions for this section:
- What is divide and conquer?
- How do you design an efficient divide and conquer algorithm?
So far, the recursive algorithms that we have seen (see text for more) are simple, and probably would NOT be done recursively. The iterative solutions work fine and are probably more intuitive and easier to implement. They were just used to demonstrate how recursion works. However, recursion often suggests approaches to problem solving that are more logical and easier than without it. For example, divide and conquer.
The idea behind divide and conquer algorithms is that a problem can be solved by breaking it down to one or more "smaller" problems in a systematic way. The subproblem(s) are usually a fraction of the size of the original problem and are usually identical in nature to the original problem. By doing this, the overall solution is just the result of the smaller subproblems being combined. If this sounds similar to recursion, that's because it's often implemented recursively. The key difference is that divide and conquer makes more than one recursive call at each level (unlike just one in the examples above).
We can think of each lower level as solving the same problem as the level above. The only difference in each level is the size of the problem, which is 1/2 (sometimes some other fraction) of that of the level above it. Note how quickly the problem size is reduced.

Integer Exponentiation
Let's look at one of our earlier recursive problems: Power function (XN). We have already seen a simple iterative solution using a for loop. We have also already seen and discussed a simple recursive solution. Note that the recursive solution does recursive calls rather than loop iterations. However both algorithms have the same runtime: we must do O(N) multiplications to complete the problem. Can we come up with a solution that is better in terms of runtime? Let's try Divide and Conquer. We typically need to consider two important things:
- How do we break up or "divide" the problem into subproblems?
- In other words, what do we do to the data to process it before making our recursive call(s)?
- How do we use the solutions of the subproblems to generate the solution of the original problem?
- In other words, after the recursive calls complete, what do we do with the results?
- You can also think of this is "how do we put the pieces back together?"
For XN, the problem "size" is the exponent N. So, a subproblem would be the same problem with a smaller N. Let's try cutting N in half so each subproblem is of size N/2. This means defining XN in terms of XN/2 (don't forget about the base case(s)). So, how is the original problem solved in terms of XN/2? Let's look at some examples.
The divide and conquer approach could look something like this, where solving XN means computing XN/2 twice (using two recursive calls), then multiplying the results together once the recursive calls return.
Possible Implementation
public long power(long X, long N)
{
if (N == 0) //base case
return 1;
else if (N == 1) //base case
return X;
else //recursive case
{
return power(X, N/2) * power(X, N/2);
}
}
|
Trace of Recursive Calls
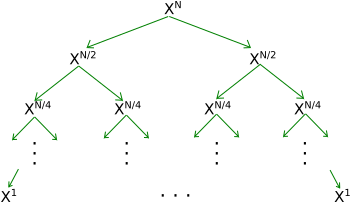
|
If you look at that tree, you might notice that you're computing XN/2 twice, XN/4 four times, XN/8 eight times, etc. You might think this is wasteful (it is). We're computing things that we already computed! Instead, you might think we could just memorize the first result (e.g. the first XN/2) and use its result any time we need it. This is called memoization, i.e. we are maintaining a memo of previously-calculated results. A memoized version of the approach could look like this:
Possible Implementation
public long power(long X, long N)
{
if (N == 0) //base case
return 1;
else if (N == 1) //base case
return X;
else //recursive case
{
long result = power(X, N/2); //memoize
return result*result;
}
}
|
Trace of Recursive Calls

|
Is this an improvement over the other approaches seen earlier? The problem size is being cut in half each time, which suggests that it takes on the order of log2(N), or O(log(N)), multiplications. See text 7.25-7.27 for more thorough analysis, but it's the same idea as the analysis for binary search. This is a big improvement over O(N)!
However, the problem with the new approach is that it assumes N is a power of 2. If N = 8, then we can easily have this:
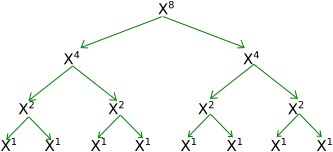 |
converts to |
 |
But what if N is not a power of 2? If N = 9, then our whole approach falls apart. Now, N/2 is not an integer. So, what's our base case now? Before, we could stop when we reached N=1 since that was simple, but now we never reach 1 (or 0, another good base case). Additionally, non-integer exponentiation is best if hard, time-consuming, and often subject to rounding errors, so it's best to avoid it if possible. So, what do we do when the N is not a power of 2? We try to convert it into a power of 2!
Let's start with at N = 9:
- We know 9 = 8 + 1.
- By the rules of exponentiation, X9 = X8 + 1 = X8 * X1.
- We now have XN (N being a power of 2) and X1 (a base case)
- We can now do the recursion described above to get X8, then multiply it by X to get X9
Ok, let's try another: N = 14. What should we do this time? Following from N=9, you might try:
- We know 14 = 8 + 1 + 1 + 1 + 1 + 1 + 1.
- By the rules of exponentiation, X14 = X8 + 1 + 1 + 1 + 1 + 1 + 1 = X8 * X1 * X1 * X1 * X1 * X1 * X1.
- We now have XN (N being a power of 2) and X1 (a base case)
- We can now do the recursion described above to get X8, then multiply it by X six times to get X14
If something seems wrong with this, that's because we're starting to transform our divide and conquer algorithm into a non-divide-and-conquer algorithm. Using this approach to convert N into a power of 2 degrades the performance of our algorithm into a O(N) algorithm just like the earlier versions of integer exponentiation we looked at. Let's take a different approach to N = 14.
We've been dividing N by 2, so we aren't necessarily concerned that N is a power of 2, just that it's divisible by 2. So, if N isn't divisible (e.g. N=9), convert it into something that is divisible by 2. Now we have two cases:
- If N is divisible by 2, XN = XN/2 * XN/2
- If N is not divisible by 2, XN = XN/2 * XN/2 * X
This is what we did for N = 9 and it worked out. Let's look at how it works for N = 14:
Possible Implementation
public long power(long X, long N)
{
if (N == 0) //base case
return 1;
else if (N == 1) //base case
return X;
else //recursive case
{
if (N % 2 == 0)
{
long result = power(X, N/2); //memoize
return result * result;
}
else
{
long result = power(X, N/2); //memoize
return result * result * X;
}
}
}
|
Trace of Recursive Calls
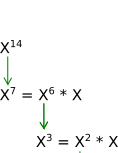
|
Code comparing this divide and conquer approach with the two we saw earlier can be found here: Power.java. The divide and conquer approach is in the method Pow3. Why do you think Pow3 has a base case of N == 0 (N.compareTo(zero) == 0)?
Binary Search
Now let's reconsider binary search, this time using using recursion with divide and conquer. Recall that the data must be in order already and we are searching for some object S.
- How do we divide?
- Cut the array in half, which is what the iterative version does
- How do we use the subproblem results to solve the original problem?
- We may not really need to do anything here at all
- What about base case? There are actually two:
- Array size is down to zero (S not found)
- Key matches current item (S found)
- What about the recursive case? Consider the middle element, M, and check if S is:
- Equal to M: you are done and you have found it (base case)
- Less than M: recurse to the left side of the array
- Greater than M: recurse to the right side of the array
This is the same logic as the iterative case. Proceeding in this fashion removes 1⁄2 of the remaining items from consideration with each guess.
Let's compare this recursive binary search to the iterative binary search (and to the sequential search). BinarySearchTest.java . Look at the number of comparisons needed for the searches. As N gets larger, the difference becomes very significant.
Read Chapter 18 of the Carrano text; it discusses both sequential search and binary search.
Tail Recursion and Recursion Overhead
- Key questions for this section:
- What is tail recursion?
- Why is it helpful to identify tail recursion?
- How do you convert from a tail-recursive method to an iterative method?
- Why would you want to convert tail-recursive methods to iterative methods?
So far, every recursive algorithm we have seen can be done easily in an iterative way. Even the divide and conquer algorithms (Binary Search, Integer Exponentiation) have simple iterative solutions. Can we tell if a recursive algorithm can be easily done in an iterative way? Yes, any recursive algorithm that is exclusively tail recursive can be done simply using iteration without recursion. Most algorithms we have seen so far are exclusively tail recursive.
Tail recursion is a recursive algorithm in which the recursive call is the last statement in a call of the method. If you look back at the algorithms we've seen so far, this is generally true (ignore trace versions, which add extra statements). The integer exponentiation function does some math after the call, but it can still be done easily in an iterative way, even the divide and conquer version. In fact, any tail recursive algorithm can be converted into an iterative algorithm in a methodical way.
Why bother with identifying tail recursion and know that it's possible to convert to an iterative method? Recursive algorithms have overhead associated with them:
- Space: each activation record takes up memory in the run-time stack
- If too many calls "stack up" memory can be a problem
- We saw this when we had to increase the stack size for BinarySearchTest.java
- Time: generating activation records and manipulating the run-time stack takes time
- A recursive algorithm will always run more slowly than an equivalent iterative version
These are implementation details that algorithm analysis ignores. An iterative implementation of binary search and a recursive implementation will have the same runtime according to algorithm analysis. Recall that algorithms are independent of programming language, hardware, and implementation details. Deciding which algorithm to use and how to implement it are two separate, but very important, questions.
If recursive algorithms have this overhead, why bother with it? For some problems, a recursive approach is more natural and simpler to understand than an iterative approach. Once the algorithm is developed, if it is tail recursive, we can always convert it into a faster iterative version (ex: binary search, integer exponentiation). However, for some problems, it is very difficult to even conceive an iterative approach, especially if multiple recursive calls are required in the recursive solution. We'll take a look at some examples in the next section.
Backtracking
- Key questions for this section:
- What is backtracking?
- How do you write a recursive, backtracking algorithm?
- What kinds of problems can benefit from backtracking?
The idea behind backtracking is to proceed forward to a solution until it becomes apparent that no solution can be achieved along the current path. At that point, undo the solution (backtrack) to a point where we can proceed forward again and look for a solution.
8 Queens Problem
In the 8 Queens Problem, you attempt to find an arrangement of queens on an 8x8 chessboard such that no queen can take any other in the next move. In chess, queens can move horizontally, vertically, or diagonally for multiple spaces.
How can we solve this with recursion and backtracking? All queens must be in different rows and different columns, so each row and each column must have exactly one queen when we are finished (why?). Complicating it a bit is the fact that queens can move diagonally. So, thinking recursively, we see that to place 8 queens on the board we need to:
- Place a queen in a legal (row, column)
- Recursively place 7 queens on the rest of the board
Where does backtracking come in? Our initial choices may not lead to a solution; we need a way to undo a choice and try another one.
Using this approach, we have the JRQueens.java program. This program also creates a graphical display to show to recursive search for the solution. The method that does the recursive backtracking is trycol, reproduced below with the display-related statements removed:
public void trycol(int col)
{
calls++; // increment number of calls made
for (int row = 0; row < 8; row++) // try all rows if necessary
{
// Don't place a queen unless it is safe to do so
if (safe(row, col))
{
// if the current position is free from a threat, put a queen
// there and mark the row and diags as unsafe
saferow[row] = false;
safeleftdiag[row+col] = false;
saferightdiag[row-col+7] = false;
(squares[row][col]).occupy();
if (col == 7) // queen safely on every column, announce
{ // solution and end execution
sol++;
System.out.println("The problem is solved!");
System.exit(0);
}
else
{
// Still more columns left to fill, so delay a bit and then
// try the next column recursively
trycol(col+1); // try to put a queen onto the next column
}
saferow[row] = true; // remove the queen from
safeleftdiag[row+col] = true; // the current row and
saferightdiag[row-col+7] = true; // unset the threats. The
(squares[row][col]).remove(); // loop will then try the
// next row down
}
}
// Once all rows have been tried, the method finishes, and execution
// backtracks to the previous call.
}
The basic idea of the method is that each recursive call attempts to place a queen in a specific column. A loop is used, since there are 8 squares in the column. For a given method call, the state of the board from previous placements is known (i.e. where are the other queens?). This is used to determine if a square is legal or not. If a placement within the column does not lead to a solution, the queen is removed and moved down one row in that column. When all rows in a column have been tried, the call terminates and backtracks to the previous call (in the previous column). If a queen cannot be placed into column i, do not even try to place one onto column i+1; rather, backtrack to column i-1 and move the queen that had been placed there.
This solution is fairly elegant when done recursively. To solve it iteratively, it's rather difficult. We need to store a lot of state information (such as for each column so far, where has a queen been placed?) as we try (and un-try) many locations on the board. The run-time stack does this automatically for us via activation records. Without recursion, we would need to store / update this information ourselves. This can be done (using our own Stack rather than the run-time stack), but since the mechanism is already built into recursive programming, why not utilize it?
Tower of Hanoi Problem
This is a simple puzzle and popular recursive algorithm problem. There are three rods. Two are empty and the third holds N disks. Each disk has a different diameter and they are stacked from widest to narrowest. Below is an image from Wikimedia Commons showing the starting setup:

The goal of the puzzle is to move the entire stack to another rod, obeying the following rules:
- Move only one disk at a time
- You can only move the top disk on a stack
- Do not place a wider disk on top of a narrower disk
How do you solve such a puzzle?
A program solving the puzzle can be found at JRHanoi.java. Most of the code in the file is dedicated to displaying the solution. The key method is solveHanoi:
public void solveHanoi(int currsize, int start, int middle, int end)
{
if (currsize == 1) // If we have only one disk, move it from start to end directly
theTowers[start].move(theTowers[end]);
moves++;
}
else // If we have more than one disk:
{
solveHanoi(currsize-1, start, end, middle); // 1) recursively move N-1 disks from start to middle,
theTowers[start].move(theTowers[end]); // 2) move last disk from start to end directly
moves++;
solveHanoi(currsize-1, middle, start, end); // 3) recursively move N-1 disks from middle to end
}
}
When a recursive algorithm has 2 calls, the execution trace is now a binary tree, as we saw with the solution to Tower of Hanoi. This execution is more difficult to do without recursion, but it is possible. To do it, programmer must create and maintain their own stack to keep all of the various data values. This increases the likelihood of errors / bugs in the code. Later, we will see some other classic recursive algorithms with multiple calls, such as MergeSort and QuickSort.
A very good demo of this can be found here: http://www.cs.cmu.edu/~cburch/survey/recurse/hanoiimpl.html.
Word Search
Let's look at one more backtracking example: Finding words in a two-dimensional grid of letters. Given a grid and a word, is the word located somewhere within the grid? Each letter must touch the previous letter and we can only move right, left, up, and down. We can solve this with recursion. Let's take a look at how.
| w |
a |
r |
g |
| b |
c |
s |
s |
| a |
a |
t |
s |
| t |
r |
y |
x |
FindWord.java gives an implementation.













