One common operation in programming is to sort. You will often have a collection of things and you will want to put them into a particular order. A simple sorting algorithm is selection sort, which finds the smallest value and swaps it into position 0. It then finds the next smallest value and swaps it into position 1. This repeats until the list is sorted. If we want to sort a list of ints, we could write selection sort that works with ints. If we want to sort a list of Strings, we could write another selection sort method that works with Strings. But, almost all of the code would be identical! The only real changes are that (1) with ints, we'd use the less than operator (<) and with Strings we'd use the compareTo method, and (2) the method's parameters would take different kinds of lists (one with ints and one with Strings). But the core of the method would be identical. It would be great if we didn't need to duplicate so much code. It would be great if we could just write one generic selection sort method that could be used on any kind of data.
Let's consider the Comparable interface. It contains just one method: int compareTo(T o) (what's the T? it's a generic placeholder for any class type...more on this soon). The return value is:
Consider what we need to know about the data for our selection sort algorithm:
Thus, as long as we write our method to take objects implementing the Comparable interface, we can sort them without knowing anything about them, other than what their compareTo method returns! The objects are almost like black boxes, only telling us how they compare to each other!
One problem though is that this still doesn't allow us to sort ints. Why not? How can we get around that?
One thing of note is that older versions of Java had a different version of the Comparable interface. Before JDK 1.5, Java did not support generic, parameterized types/interfaces/methods, so the Comparable interface's compareTo method took an Object to compare. While we will be using more modern versions of Java, this is important to know in case you end up developing in an older Java environment.
The introduction of generics helped make a programmer's job easier. To understand that, let's look at the two versions of the Comparable interface:
Both versions allow arbitrary objects to be compared. The difference is that in the parameterized version ("new Java"), the types of the objects can be established and checked at compile-time. With the original version, this could not be done until run-time.
To see this consider the parameter to the compareTo() method. In the orginal version it is Object. In the parameterized version it is T (i.e. whichever type is passed into the parameter of the interface). Now, for 2 objects, C1 and C2, consider the call:
C2 can be any Object. So if C2's object was incompatible with C1's object (i.e. apples and oranges) this problem would not be known until program execution.C2 and make sure it matches with the type set for T in the definition of compareTo. If the types are incompatible, the compiler will give an error.Why do we care? Compilation errors are typically much easier to resolve than run-time errors. We'd like to "push" as much of the error-checking as possible to compile-time, while preserving the flexibility of the language. Parameterized types allow this to be done.
For an example, see: PeopleSort.
As mentioned above, Java allows for generic interfaces, classes, and methods. We saw an interface example with Comparable<T>. Let's look at a simple class example and a simple method example. Let's try to (very simply) mimic the functionality of a Java array:
Let's see how to do this with Java Generics. For simplicity, we will start with a class that does everything above, but does not use generics (so, it can't hold any Java type yet). You should already know how to do everything below from CS/COE 401:
Note that MyArray is not really a useful type, it is just meant to demonstrate parameterized Java types.
We are familiar with data types in Java, such as primitive data types (e.g. int, double, boolean) or reference types (e.g. String, StringBuilder, File). We can think of these as a combination (or encapsulation) of two things:
For example, the int type in Java. We can think of it simply as whole numbers, represented in some way in the computer, but this would be incomplete. What makes integers useful is the operations that we can do on them, for example +, -, *, /, % and others. It is understanding the nature of the data together with the operations that can be done on it that make ints useful to us. We, of course, also have Integer and BigInteger.
So where does the abstract part come in? Note that in order to use ints in our programs, we only need to know what they are and what their operations are. We do not need to know their implementation details. Does it matter to me how the int is represented in memory? Does it matter how the actual division operation is done on the computer? For the purposes of using integers effectively in most situations: NO! These are abstracted out of our view!
More generally speaking, an ADT is a data type (data + operations) whose functionality is separated from its implementation. The same functionality can result from different implementations. Users of the ADT need only to know the functionality. Naturally, however, to actually be used, ADTs must be implemented by someone at some point. The implementer must be concerned with the implementation details. In this course, you will look at ADTs both from the user's and implementer's point of view.
This should be familiar to you. We have already discussed the idea of data abstraction from classes. The difference is that abstract data types are language-independent representations of data types. They can be used to specify a new data type that can then be implemented in various ways using different programming languages. Classes are language-specific structures that allow the implementation of ADTs. Classes only exist in object-oriented or object-based languages.
A given ADT can be implemented in different ways using different classes. We will see some of these soon, such as Stack, Queue, SortedList can be implemented in different ways. In fact, a given class can be used to represent more than one ADT. The Java class ArrayList can be used to represent a Stack, Queue, Deque and other ADTs.
Consider interfaces again, where you specify a set of methods, or, more generally a set of behaviors or abilities. You do not specify how those methods are actually implemented. You don't even specify the data upon which the methods depend. Thus, interfaces fit reasonably well with ADTs. One difference though is that ADTs do specify the data, but we can infer much about the data based on the methods.
The text will typically use interfaces as ADTs and classes as ADT implementations. Using the interface, we will have to rely on descriptions for the data rather than actual data. The data itself is left unspecified and will be detailed in the class(es) that implement the interfaces. This is ok since the data is typically specific to an implementation anyway. One good example of this is the Map ADT (which other programming languages call "dictionary") and two of Java's implementations: HashMap and TreeMap.
For another example, the ADT Stack:
At this level (where we just describe the actions of the ADT), we don't care how the objects are stored.
Many ADTs (especially in this course) are used to represent collections of data. A collection is when multiple objects are organized and accessed in a particular way. The organization and access is specified by the ADT (through interfaces in Java). The specific implementation of the data and operations can be done in various ways (through classes in Java). Throughout this term, we will examine many data structures.
Think of a real bag in which we can place things. There are no rules about:
However, we will make it homogeneous by requiring the items to be the same class or subclass of a specific Java type.
Let's look at the interface:
Note what is not in the interface:
The interface also does not explicitly include things that probably should be included, such as:
We typically have to handle these via comments, which this interface does provide.
Let's examine one method in some detail:
We want to consider specifications from two points of view:
add(newEntry) example, we might have:
add(newEntry) example, we might have:
newEntry is not a valid objectadd(newEntry) method?
The Bag is a simple ADT, but it does have its uses. One example is to generate some random integers and count how many of each number were generated. There are many ways to do this, but one is with a bag. See BagExample. Is BagExample.java the most efficient way to generate the random integers and count the number generated? That depends on how the Bag ADT is implemented.
Ok, now we need to look at a Bag from the implementer's point of view. The implementer must answer the questions:
The implementation of the operations will be closely related to the representation of the data. Minimally, the data representation will "suggest" ways of implementing the operations. Note that these implementation questions (and the ones below) are (mostly) irrelevant to the client, but are quite important to the implementer. Why might they be relevant at all to the client (the one using the ADT)?
Let's first consider using an array to represent/hold the data. This makes sense since it can store multiple values and allow them to be manipulated in various ways. Perhaps a field in our Bag like:
Ok, so an array appears to answer the first question (how to represent the data), but there's still more to consider. We know the size of an array object is fixed once it is created. We also know that our Bag must be able to change in size (with adds and removes), meaning we must make more decisions about how to implement the array in our bag. Thus we need to create our array, then keep track of how many locations are used with some other variable:
But how big should we make the array? If it's too small, then we could run out of room quickly or need to resize soon (which takes a lot of time). If it's too large, then we're wasting a lot of memory. We have two approaches to take. We can either use a fixed size and when it fills it fills, or we can dynamically resize when necessary (transparently).
The idea of a fixed-size array is to initialize the array in the constructor. Have the physical size be passed in as a parameter; this becomes the size of the array. Then the logical size (i.e. the number of array elements actually used) is maintained by the numberOfEntries variable. Once created, the physical size is constant as long as the list is being used. Once the array fills (i.e. logical size == physical size), any "add" operations will fail until space is freed (through "remove" or "clear").
The advantage to this approach is that it is easy for the ADT programmer to implement. It does come with some disadvantages though. The first is that the ADT user (programmer) may greatly over-allocate the array, wasting space but hopefully never running out of room. The second is that the program user (non-programmer) may run out of room at run-time, especially if the ADT user does not over-allocate. Neither of these are desirable. Dynamically resizing the array is a solution to this problem, but let's first consider the implementation of this fixed-size array since the dynamic solution will be very similar.
Let's start with the simple method we have been discussing:
Recall our data:
private T [] bag;private int numberOfEntries;How about a bit more complicated operation?
What do we need to do here?
The approach to implementing the other methods should be the same:
See the text or the comments in the interface for a discussion of the other operations. For the complete implementation, see ArrayBag.java in BagExample. Notice the use of private methods. Why do you think those were created? Why do you think they were created private?
The basic idea with a dynamic size array is that the array is created with some initial size, then resized when necessary. The constructor can allow the programmer to pass the initial size in, or we can choose some default initial size. If this array becomes filled, we must:
Some questions we must consider are:
On the question of how big to make the new array, it clearly must be bigger than the old array, but how much bigger? What must we consider when deciding the size? Well, if we make the new array too small, we will have to resize often, causing a lot of overhead. If we make the new array too large, we will be wasting a lot of memory. For now, let's just make the new array twice the size of the old one. This way we have a lot of new space but are not using outrageously more than we had before. We will see more specifically why this was chosen later.
On the question of how to copy, this is pretty easy. We just start at the beginning of the old array and copy index by index into the new array. Note that we are copying references, so the objects in the new array are the same objects that were in the old array.
What do you think happens to the old array?
Let's take a look at what's happening (on the board). Now, let's look at how the add(T newEntry) and the remove(T anEntry) methods are changed (if they need to be). A complete implementation of the dynamic size array version of the bag is in ResizableArrayBag.java in the zip file: BagExample2.zip. There is also BagImplementationComparisons.java to compare the use of both implementations.
Let's now look at the implementations of the add method:
Notice that the typical case (where there is already enough room in the bag) is identical. In both cases, it's:
The big change is what to do when the bag is full:
Finally, the dynamic size implementation of the add method always returns true. Why does it do that? Why don't we change it to a void method?
The dynamic size implementation of the add method calls the doubleCapacity method. Let's look at what that method does:
A couple of notes about this method:
checkCapacity() makes sure size is not too big (the book is concerned about that, we haven't been in lecture and that's ok). You can check the source code linked above for its implementation.numberOfEntries in this method. Why don't we?Do you think any changes need to be made to the remove(T anEntry) method? Why or why not? If changes need to be made, what would they be?
There are two approaches to using memory when building a data structure. Both bag implementations above use contiguous memory: locations are next to each other in memory. Given the address of the first location, we can find all of the others based on an offset from the first. Consider the array declaration:
The memory looks like this:
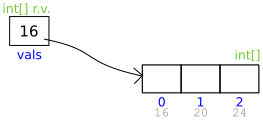
The reference variable holds the address of the array. Under each element of the array is the array index (0, 1, 2) and the memory address of each position in the array (16, 20, 24). The first element is at position 16 in memory, the second is at position 20, and the third at position 24. The position of each element is 4 bytes greater than the position of the previous position because the size of an int is 4 bytes.
Contiguous memory has many benefits:
val[i] can be done in a single operation. Its position is calculated by: Unfortunately, there are also drawbacks to contiguous memory:
We will discuss the details of "how much" time is required later, when we talk about algorithm analysis.
Focusing on these drawbacks, is there an alternative way of storing a collection of data that avoids these problems? What if we can allocate our memory in small, separate pieces, one for each item in the collection? Now we allocate exactly as many pieces as we need. Now we do not have to shift items, since all of the items are separate anyway.
But how do we keep track of all of the pieces? We let the pieces keep track of each other! Let each piece have 2 parts to it:
This is the idea behind a linked-list:
The idea behind a linked list is that if we know where the beginning of the list is and each link knows where the next one is, then we can access all of the items in the list. Our problems with contiguous memory now go away. Allocation can be done one link at a time, for as many links as we need. New links can be "linked up" anywhere in the list, without needing to shift elements around to make room.
The key to implementing a linked list is how each link is implemented. As stated above, two parts are needed, one for data and one to store the location of the next link. We can do this with a self-referential data type:
"Node" is a common name for a link in a linked list. Why do you think the node is called "self-referential"?
There are variations of the linked list, but for now we'll talk about the simplest: singly linked list. Links go in only one direction, making it easy to go from beginning to end but impossible to go backwards. The implementation is developed in Chapter 3, but let's take a quick look at some of it:
Note that the LinkedBag has a private inner class called Node. Why do you think it's private? Why do you think Node's constructors are private?
Why is it done this way? Since Node is declared within LinkedBag, methods in LinkedBag can access private declarations within Node. This is a way to get "around" the protection of the private data. LinkedBag will be needing to access data and next of its Nodes in many of its methods. We could write accessors and mutators within Node to allow this access, but it is simpler for the programmer if we can access data and next directly. However, they are still private and cannot be accessed outside of LinkedBag. On the downside, with this implementation, we cannot use Node outside of the LinkedBag class, because it is a private class declared within LinkedBag.
Now let's see how we would implement some of our BagInterface methods using this linked list version of a bag. We'll start with the add method:
Let's take a look at how this works with a few examples on the board. Are there any special cases that the LinkedBag implementation should consider (that it isn't)?
How does this compare to the add method from the array implementation? For comparison, here's the dynamic size array implementation of add:
Are there any similarities between the two versions? What are the differences? Are any of those differences a problem?
Let's take a look at another method, this time one that uses a loop. Let's look at the contains(T anEntry) method, which determines whether the bag contains anEntry. Just like for the array, we will use sequential search. Just like for the array, we start at the beginning and proceed down the bag until we find the item or reach the end.
So what is different? How do we "move down" the bag? How do we know when we have reached the end? Let's look at the code.
Notice that the loop will terminate when either found == true or null is reached (in which case found == false).
Let's look at one more operation:
We want to remove an arbitrary item from the Bag. How do we do this? Think about the contains() method that we just discussed. How is remove similar and how is it different?
Consider again the properties of a Bag. One property is that the data is in no particular order. So, we could remove the actual Node in question, but perhaps we can do it more easily. The front Node is very easy to remove (see example in lecture). So let's copy the item in the front Node to the Node that we want to remove. Then we remove the front Node. Logically, we have removed the data we want to remove. Keep in mind that the Nodes are not the data, they are simply a mechanism for accessing the data. Also keep in mind that this would NOT be ok if the data need to stay in some kind of order.
There are other methods that we have not discussed. Look over them in the text and in the source code. See LinkedBag.java for the linked list implementation of a bag and BagExample2.java for an example comparing the various bag implementations; both can be found in: BagExample3.zip.
Node as a Separate ClassNode class and LinkedBag class?Some object-oriented purists believe it is better to never "violate" the private nature of a class' data. If done this way, the Node class must also be a parameterized type:
Access to next and data fields must now be done via accessors and mutators, so these must be included in the Node<T> class. See Node.java for complete implementation.
Let's look at a method in LinkedBag.java we have already discussed, but now using this variation: contains(anEntry). The differences from the previous version are shown in red.
| << Previous Notes | Daily Schedule | Next Notes >> |