CS1674: Homework 8

Due: 11/15/2023, 11:59pm

This assignment is worth 50 points.

In this assignment, you will implement a subset of the operations that are performed in a convolutional neural network.

Part I: Network Activations [10 points]

In this part, you will compute some network activations using a given input and fixed network weights. Use the following network diagram (similar to the one we saw in class, but without bias terms).

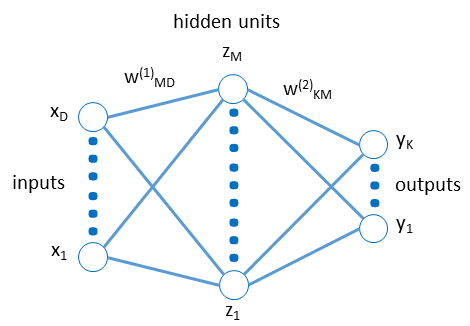
The following are the input pixel values, and the weight values.

x₁ = 0	w⁽¹⁾₃₁ = 0.72
x₂ = 10	w⁽¹⁾₃₂ = 0.1
x₃ = 2	w⁽¹⁾₃₃ = 0.35
x₄ = 30	w⁽¹⁾₃₄ = 0.3
w⁽¹⁾₁₁ = 0.5	w⁽²⁾₁₁ = 0.7
w⁽¹⁾₁₂ = 0.6	w⁽²⁾₁₂ = 0.45
w⁽¹⁾₁₃ = 0.4	w⁽²⁾₁₃ = 0.5
w⁽¹⁾₁₄ = 0.3	w⁽²⁾₂₁ = 0.17
w⁽¹⁾₂₁ = 0.02	w⁽²⁾₂₂ = 0.9
w⁽¹⁾₂₂ = 0.25	w⁽²⁾₂₃ = 0.8
w⁽¹⁾₂₃ = 0.4
w⁽¹⁾₂₄ = 0.3

In a script activations.m:

[3 pts] First, encode all inputs and weights as matrices/vectors in Matlab. In our example, D=4, M=3, K=2.

[3 pts] Second, write code to compute and print the value of z₂, if a tanh activation is used. You can use Matlab's tanh function.

[4 pts] Third, write code to compute and print the value of y₁, if RELU activation is used at the hidden layer, and sigmoid activation is used at the output layer. Don't use the Matlab functions, instead use the formulas for these functions that were shown in class and implement them yourself. You don't have to implement the exp function, just call it.

Part II: Loss Functions [10 points]

In this part, you will compute two types of loss functions: hinge loss and cross-entropy loss. You will use three different sets of weights W, each of which will result in a different set of scores s = W*x for four data samples, where x is of size 25x1, W is of size 4x25, and s is of size 4x1. Based on the computed losses, you have to say which set of weights is better. The weights and samples are in this file. The first sample (x₁) is of class 1, the second of class 2, the third of class 3, and the fourth of class 4.

[3 pts] Write a function [loss] = hinge_loss(scores, correct_class) to compute the L_i loss for an individual sample.
Inputs:
- scores is a 4x1 set of predicted scores, one score for each class, for some sample, and
- correct_class is the correct class for that same sample.
Output:
- loss is a scalar measuring the hinge loss, as defined in class, given these scores and ground-truth class.

[3 pts] Write a function [loss] = cross_entropy_loss(scores, correct_class) to compute the L_i loss for an individual sample. The inputs are defined as above. The output is analogous, but computing cross-entropy loss rather than hinge loss.

[4 pts] Write a script losses.m to compute and print each type of loss (hinge or cross-entropy) for each weight matrix. Then, in a file answers.txt, say which weight matrix is the best one, (1) according to the hinge loss, and (2) according to the cross-entropy loss.

Part III: Gradients [10 points]

In this part, you will compute the numerical gradient for the first weight vector from the previous part, and a weight update.

[8 pts] Write a script gradient.m to loop over the dimensions of the weight vector and numerically compute the derivative for each dimension, as shown in class. Then concatenate the derivatives together, and output the resulting vector as the gradient. Use the hinge loss to compute the loss for that weight vector over all examples. Use h=0.000001.

[2 pts] In the same script, also compute a weight update (one iteration) with learning rate of 0.01.

Tips:

Make W₁ into a vector via W1(:). Use reshape to reshape any intermediate W1_plus_h (needed in the process of computing a derivative) back into a 4x25 matrix.
Make sure to change each dimension of the weight vector one at a time, so store the original version of the weight vector before any changes were made to it, and reset the weight vector to that original each time you loop over the dimensions.

Part IV: ConvNet Operations [20 pts]

In this part, you will compute the output from applying a single set of convolution, non-linearity, and pooling operations, on two small examples. Below are your image (with width = height = N = 9) and your filter (with width = height = F = 3).

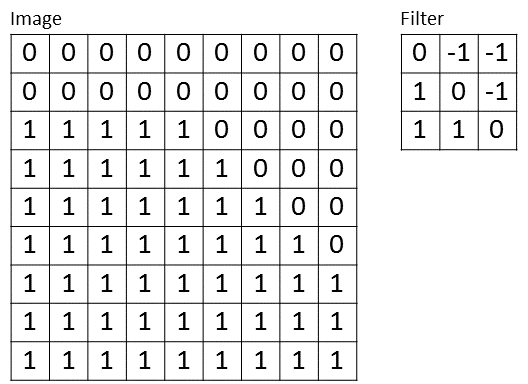
[7 pts] Write a function [Output] = my_conv(Image, Filter, Padding, Stride) that computes the output of applying a filter over an image, with given padding and stride. You are not allowed to use any convolution-related Matlab functions except element-wise multiplication between two matrices, followed by summation. You are allowed to implement correlation instead of convolution as a simplification.
Inputs:
- Image is a grayscale single-channel image, e.g. the one shown above (don't hard-code it in your function).
- Filter is a single-channel filter, e.g. the one shown above (don't hard-code it in your function).
- Padding is a scalar saying how much padding to apply above/below and to the left/right of the Image.
- Stride is a scalar saying what stride to use to advance over the Image during convolution.
Output:
- Output is the single-channel matrix resulting from the convolution operation.

[7 pts] Write a function [Output] = my_pool(Input, Pool_Size) that computes the output of non-overlapping max-pooling over Pool_SizexPool_Size regions of the input. Again, you are not allowed to use built-in Matlab functions that compute pooling.
Inputs:
- Input is a square matrix, which you should assume to be the result from applying RELU on the output from convolution.
- Pool_Size is a scalar saying over what size of regions to compute max (e.g. use 2 for pooling over 2x2 regions).
Output:
- Output is the single-channel matrix resulting from the max-pooling operation.

A script test_cnn_ops.m is provided to test your two functions in two scenarios. When you run it, it will encode the example image and filter above, call your functions (conv -> relu -> pool) and save the output variables output1, output2 in a file outputs.mat. Run this script and submit the saved output file. The tests in the script are as follows:
1. [3 pts] Test 1:
  - First, apply convolution using no padding, and a stride of 2 (in both the horizontal and vertical directions).
  - Second, apply a Rectified Linear Unit (ReLU) activation on the previous output.
  - Third, apply max pooling over 2x2 regions on the previous output.
2. [3 pts] Test 2:
  - First, apply convolution using padding 1, and a stride of 4.
  - Second, apply a Rectified Linear Unit (ReLU) activation on the previous output.
  - Third, apply max pooling over 3x3 regions on the previous output.

Submission:

activations.m
hinge_loss.m
cross_entropy_loss.m
losses.m
answers.txt
gradient.m
my_conv.m
my_pool.m
outputs.mat