CS 1501 Previous Final Exam Solutions

For all questions, be sure to show your work.  Answers without work will not receive full credit.

1)      (20 points – 2 points each) Fill in the Blanks. Complete the statements with the MOST APPROPRIATE word(s) and/or phrase(s).

 

a)      In order to save space in the hash table storing dictionary entries for the LZW compression algorithm, rather than storing the entire string in the hash table, we instead store a(n) _____prefix code_________  and a(n) ____append character_____ that together indicate the string with a constant amount of space.

b)      During BFS and PFS, some vertices are on the fringe, which means that ____they have been seen but not yet visited___.

c)      DFS on a graph with V vertices and E edges runs in time ______Theta(V + E)________ with an adjacency list and in time ______Theta(V2)___________ with an adjacency matrix.

d)      A graph G is said to be biconnected if ___there are at least two distinct paths between all vertex pairs__.

e)      The only difference between Prim's MST algorithm using PFS and Djikstra's Shortest Path algorithm using PFS is _______the way the priority is determined________.

f)       A sequence of N Inserts followed by N DeleteMins on a sorted array will have a total run-time of Theta(_____N2______).

g)      A sequence of N Inserts followed by N DeleteMins on a min-heap will have a total run-time of Theta(____NlgN____).

h)      One rule for a valid flow in a network graph is: For All (u,v) in V, f(u,v) =  –f(v,u).  This means ____ if a positive flow is going from u to v, than an equal weight negative flow is going from v to u_______.

i)        The Ford-Fulkerson solution to the Network Flow problem involves finding a(n) ______augmenting path_____ for the network, updating the residual network, and repeating until no ______augmenting path________ (same answer as first part) can be found.

j)        We can prove a problem is NP-complete either from scratch, or we can use reduction, by which we ____show that a problem known to be NP-complete is transformable to the new problem in polynomial time___.

 

2)      (10 points – 2 points each) Indicate if each of the following statements is TRUE or FALSE.  For FALSE statements, INDICATE WHY THEY ARE FALSE.

 

a)      An advantage of an adjacency matrix representation of a graph is that all neighbors of a vertex can be found in time Theta(V) (where V is the number of vertices in the graph).  FALSE – this is a disadvantage if the graph is sparse (since a vertex may have << V neighbors).

b)      NP-Complete problems are problems that are known to require exponential run-times.  FALSE – it is believed to be so but it has not been proven.

c)      If I discover a true polynomial algorithm that solves the Traveling Salesman Problem, I will have proved that P = NP.  TRUE

d)      The recursive solution to the Fibonacci Sequence is an example of a algorithm that is both elegant and efficient in its run-time.  FALSE – the recursive Fibonacci solution has an exponential runtime.

e)      The dynamic programming solution to the Subset Sum problem runs in polynomial time.  FALSE – it runs in pseudo-polynomial time (it can be exponential for some problem instances).

3)      (16 points – 8 + 8) Consider the LZW compression algorithm that we discussed in lecture. 

a)      Consider a file with 3,000,000 letter As in it (no other characters, except for the end of file character).  How large a codeword size (in terms of bits) will be needed so that we DO NOT run out of codewords in the process of compressing this file?  Justify your answer thoroughly for full credit.  Hint: Trace it for the first few cycles to see the trend, then use some math to determine the answer.

 

Answer: Each match will increase by one letter in length from the previous match.  Thus, the first codeword output will represent A, the second will represent AA, the third will represent AAA and more generally the ith codeword will represent i As.  If K codewords are output then K insertions into the dictionary are performed.   We first want to solve for K such that

 

              K

Sum  i  = 3000000

                   i = 1

 

      Since we know that the sum generally solves to K(K+1)/2, we next want to solve for K such that

 

                  K(K+1)/2 = 3000000

     

This is difficult to solve exactly without the quadratic formula, but luckily we do not need to solve it exactly.  We know that an N-bit codeword can represent 2N different codewords.  Thus we only need to find an approximate answer for K within a power of 2.  If we ignore the +1 in the formula we get

 

            K2/2 = 3000000 or K2 = 6000000 which means K = sqrt(6000000)

 

We know sqrt (4000000) = 2000 and sqrt(9000000) = 3000.  This puts K between 2000 and 3000.  With N = 11 bits we can represent 2048 codewords and with N = 12 bits we can represent 4096 codwords.  Since 256 codewords are needed for the original ASCII set, we will definitely need more than 2048 codewords, so the answer is 12 bits.

 

 

b)      Consider a file containing the following codewords (stored in binary):

65  66  65  67  256  260

Trace the LZW decoding process for the file (in the same way done in handout lzw2.txt).  Assume that the extended ASCII set will use codewords 0-255.  For each step in the decoding, be sure to show all of the information indicated below.  Note: The ASCII value for 'A' is 65.

 

STEP     CODEWORD INPUT    STRING OUTPUT     (CODE, STRING) ADDED TO DICTIONARY

----     --------------    -------------     ----------------------------------

         1                       65                              'A'                                                 --

         2                       66                              'B'                                                (256, 'AB')

         3                       65                              'A'                                                (257, 'BA')

         4                       67                              'C'                                                (258, 'AC')

         5                      256                             'AB'                                             (259, 'CA')

         6                      260                             'ABA'                                           (260, 'ABA')

 

4)      (8 points) An array representation of a min-heap data structure is shown below.  Draw the resulting array after the operation  Insert(20).  Show your work.

1

2

3

4

5

6

7

8

9

10

 

15

25

20

30

60

55

35

45

50

80

 

 

 

1

2

3

4

5

6

7

8

9

10

11

15

20

20

30

25

55

35

45

50

80

60

 

Initially 20 is placed into the last index (first available leaf from left in bottom level of tree).  It then does an upheap(), swapping with its parent in index 5 and then again in index 2. 

 

 

5)      (10 points – 8 + 2)  Consider the graph below.  Assume the vertices are stored in alphabetical order, and that the edges are stored in alphabetical order for each vertex.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


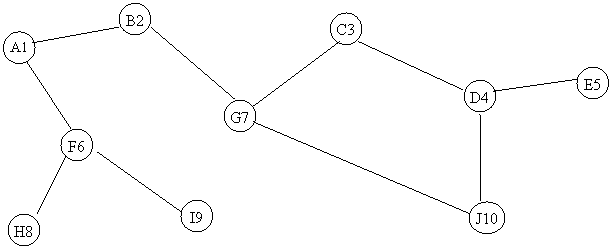
a)      Complete the table below, as it would look after a Breadth-First Search Spanning Tree (starting from vertex A1) were created for the graph.  val[] is the BFS number for the vertex, and dad[] is the parent vertex in the BFS tree.  Show your work above or in the space below the table for partial credit.

 

 

A1

B2

C3

D4

E5

F6

G7

H8

I9

J10

val

1

2

7

9

10

3

4

5

6

8

dad

--

A1

G7

C3

D4

A1

B2

F6

F6

G7

 

 

 

 

b)      Identify all of the articulation points in the graph.

Answer: A, B, G, D, F

 

6)      (10 points -- 8 + 2)  Consider the complete weighted graph below and an initial tour of the graph ABCDEA of weight 25.

 

 

 

 

 

 

 

 

 

 

 

 


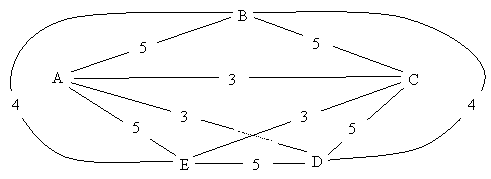
a)      Show ALL POSSIBLE edge swaps in the 2-OPT neighborhood of this tour, listing the potential improvement (if any) for each over the original tour.

 

OLD                            NEW                            CHANGE

-----                              ------                             ------------

            AB, CD (10)                 AC, BD (7)                      -3

            AB, DE (10)                 AD, BE (7)                      -3

            BC, DE (10)                 BD, CE (7)                      -3

            BC, EA (10)                 BE, CA (7)                      -3

            CD, EA (10)                 CE, DA (6)                      -4     

 

 

b)      Indicate which of the possible tours above is actually chosen, show the new resulting tour and list its total weight.

 

The last neighbor is the best, with an improvement of 4, giving new tour ABCEDA with a weight of 21.

 

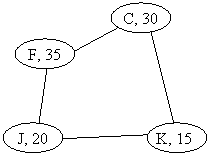
7)      (8 points) Consider the weighted graph below. The numbers are the edge capacities. S is the source vertex and T is the sink vertex.

 

 

 

 

 

 

 

 

 

 

 

 


Using the Priority First Search implementation of the Ford-Fulkerson algorithm, show EACH AUGMENTING PATH generated (in the correct order that the paths are generated), the amount of flow for each path, and the Maximum Flow for the graph.  For partial credit, be sure to SHOW YOUR WORK.

 

Answer:

 

Path                      Flow

------                     ------

SBCT                   80

SAT                      50

SACBT                40

SBT                      20

 

TOTAL:              190

 

 

8)      (10 points) Consider an unweighted graph that may or may not be connected.  Assume that each VERTEX in the graph is storing a single, positive integer.  Using a modification of the DFS algorithm for adjacency matrices, write C++ or Java code that will indicate and write out the vertex with the minimum data for each connected component in the graph.  For example, given the graph below, the output of your code should be:

C.C. 1: Minimum Element B, 15

C.C. 2: Minimum Element K, 15

C.C. 3: Minimum Element D, 5

 

 

 

 

 

 

 


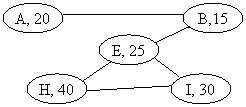
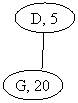
Below is some (modified) code from the text with comments that you should use as a starting point.

 

Data that is already initialized for you to use:

M[][] – adjacency matrix for the graph

label[] – char array that gives the letter for each vertex (1 is A, 2 is B, etc)

data[] – int array storing the integer data for each vertex

val[] – array to determine if a vertex has been visited or not

 

void search()  // Main search function – all of your output should be done

{              // from here. 

    id = 0;    // Assume id is a global variable

    for (int k = 1; k <= V; k++)  // V is the number of vertices in the graph

           val[k] = unseen;       // Initialize all vertices to unseen

    // Loop here to call find_min for each connected component and output result

    int CC = 1;

    for (int k = 1; k <= V; k++)

    {

         if (val[k] == unseen)

         {

              int min = find_min(k);

              char minc = label[min];

              int mini = data[min];

              cout << "C.C. " << CC << ": Minimum Element " << minc << "," << mini << endl;

              CC++;

         }

    }

 

}

 

int find_min(int k)     // Recursive DFS, but now with a return int that

{                       // is the index of the minimum data for that call.

    val[k] = ++id;      // val set to DFS number of vertex.  This number

                        // is only important in determining what has been visited

 

    int min = k;

    for (int t = 1; t <= V; t++)

    {

         if (M[k][t] != 0)

             if (val[t] == unseen)

             {

                 int rmin = find_min(t);

                 if (data[rmin] < data[min])

                      min = rmin;

             }

    }

    return min;

 

}

9)      (8 points – 4 + 4)  Consider a weighted graph with V vertices and E edges

a)      State and thoroughly justify the minimum and maximum values for E in terms of V.

 

Answer: Minimum E is 0, since no minimum edge requirement is specified for a graph.  Maximum E depends on if the graph is directed or undirected.  For a directed graph, typically self-edges are allowed, and edge AB != edge BA.  Thus, each vertex can have V edges for VxV = V2 total edges.  For an undirected graph, typically self-edges are not allowed and edge AB == edge BA.  Thus, each of the V vertices can connect to V-1 other vertices, for V(V-1) connections.  Since the connections count each edge twice, the total is V(V-1)/2.

 

b)      State, in terms of V and E, the run-time of Prim's MST algorithm using PFS when using an adjacency list and when using an adjacency matrix (2 answers required).

 

Answer:    PFS MST for Adjacency list: Theta((V + E)lg V)

                  PFS MST for Adjacency matrix: Theta(V2)