Weighted, Directed Graphs & Adjacency Matrices

A graph may be thought of as a set of nodes (or vertices) and edges. In a weighted, directed graph, the nodes and the edges may carry a label or some information. Often the nodes will carry a label and the edges will carry a value (weight or cost).
In a directed graph an edge has direction. It goes from one node to another node.

In the graph example below, the weighted edges (representing distance) go from one city to another city. The edges have direction

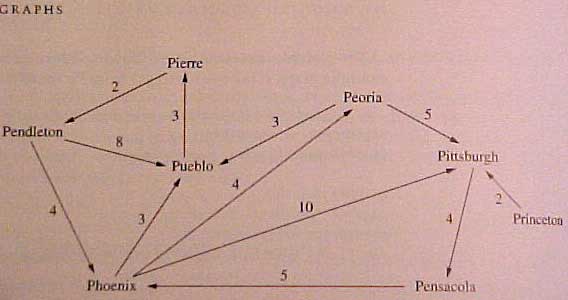
Such a graph G can be represented via an adjacency matrix. In such a matrix the row and column names are the names of the nodes. The value at each G[row][col] position represent the cost or weight of the edge between the two nodes. If there is no edge between two nodes then an impossibly large value such as infinity ( oo ) or a large constant is stored to represent the fact that no edge exists between the 2 nodes. Also note a weight of 0 between any node to itself.

The adjacency Matrix for the above example would thus be:

City #         0   1   2   3   4   5   6   7
--------------------------------------------
0 Pendeleton   0   oo  oo  4   oo  oo  oo  8
1 Pensicola    oo  0   oo  5   oo  oo  oo  oo
2 Peoria       oo  oo  0   oo  oo  5   oo  3
3 Phoenix      oo  oo  4   0   oo  10  oo  3
4 Pierre       2   oo  oo  oo  0   oo  oo  oo
5 Pittsburgh   oo  4   oo  oo  oo  0   oo  oo
6 Princeton    oo  oo  oo  oo  oo  2   0   oo
7 Pueblo       oo  oo  oo  oo  3   oo  oo  0

Filling an adjacency Matrix from an input file

Your 1st assignment will require you to read a text file graph.txt into a matrix that represents the adjacency matrix of a graph. The adjacency matrix input file for our Lab #10 looks like this: This format is an adjacency list (vs. adjacency matrix). It is more compact on a sparse graph that is not highly connected.

The first number in the file represents how many nodes the graph has. The remaining lines are triplets of the form (source-node, dest-node, edge-weight). In the above input file, the second line of the file reads as follows:

0 1 10
There is an edge from node 0 to node 1 and the weight of the edge is 10.

The third line of input reads as follows:

0 6 2
There is an edge from node 0 to node 6 and the weight of the edge is 2.

and so on for every remaining triplet line in the input file.

From this input file is obvious what is to be done. We must dimension a 8 x 8 matrix and for every triplet (source, dest, weight ) we read in, we will store

G[source][dest] = weight  // where G is some 2D array indexed with [][] braces

Properties of directed graphs

A nodes of a directed graph has certain properties as a result of it's edges having direction. For a directed graph, we can define the following terms:

out-degree - the number of edges leaving the vertex
in-degree - the number of edges entering the vertex
degree - the number of edges entering and leaving the vertex

Your Lab #9 assignment is to write a graph class to containing a 2D array to store the connection data and to implement among others) the above 3 private methods. After doing so and testing your implementation, you will implement the following 6 public methods in the Graph.java file. These 6 methods are composed on the above 3 private methods. They require that the above 3 methods are already written and tested. Don't write the 6 below until you test the 3 above.

Max Out Degree - the maximal number of edges leaving any single vertex
Min Out Degree - the minimal number of edges leaving any single vertex
Max In Degree - the maximal number of edges entering any single vertex
Min In Degree - the minimal number of edges entering any single vertex
Max Degree - the maximal number of edges entering/leaving any single vertex
Min Degree - the minimal number of edges entering/leaving any single vertex

For the input file graph.txt -- the correct answers are

Max Out Degree - 3
Min Out Degree - 1
Max In Degree - 4
Min In Degree - 0
Max Degree - 5
Min Degree - 2

In class exercise

Draw and fill in the 2D array that represents the above graph file (sparse format).
Describe an algorithm for computing the in-degree, out-degree and degree of a given node
Describe an algorithm for computing the min and max in/out/degree of the graph?

What are the data members of our Graph class?
- a Matrix of ints representing cost/weight for that edge
- Counters for how many edges etc.
What should the Constructor do?
- Initialize the number of rows and columns
- Initialize each element to the NO_EDGE value (use some constant)
What other methods are need to represent our graph concept?
- addEdge( scr, dest, weight) // puts a weight value there
- removeEdge( src, dest ) // pit a NO_EDGE val there
- hasEdge( src, dest ) // T/F is there an edge here ?
- readEdgeFile( fileName ) // read in a sparse format graph input file
- toString() // dumps a 2x2 text table (Matrix) of the edges