c1131 - page 1 of 1

11.3. An AVL Tree and Balancing Height

In this section, we study the AVL tree. In practical application, there are many searches,

insertions and deletions in a tree with n nodes. However, since we do not know order n and the

tree may not be balanced, we need large time to manipulate a tree with n nodes. Thus in order to

optimize search times, we keep the tree balancing at all times. An AVL tree has O(log n) in the

worst case to manipulate searches, insertions and deletions in a tree with n nodes.

11.3.1. Definition

In complete binary tree with node n, we know already that the left and right subtrees of any

node have the same height. In this section, we try to make a search tree that the height of every

left and right subtree never differ by more than 1 by changing a search tree.

Definition: An AVL tree is a binary search tree that is either empty or that consists of two AVL

subtree, left subtree and right subtree, whose heights differ by no more than 1 as follow.

| H

–

HR | =

is the height of the left subtree and HR is the height of the right subtree.¦

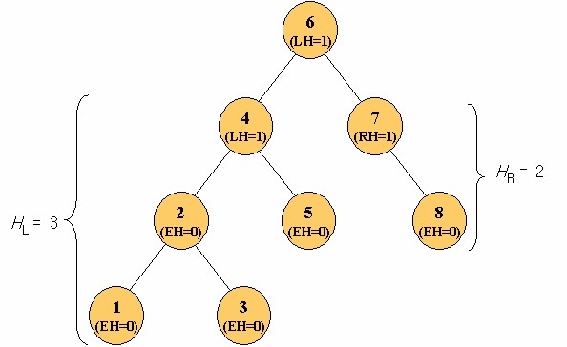
Fig. 11.21 shows an example of an AVL trees to satisfy the definition. In Fig. 11.21, LH, RH and

EH is balance factor that means a left-high node, a right-high node and equal respectively.

LH=1 of root 6 means that left subtree of root 6 has height 1 more than its right subtree. RH=1 of

node 7 means that its right subtree has height 1 more than left subtree. EH=0 is same height.

Fig. 11.21. An example of an AVL tree

In Fig. 11.21, since the height of the left subtree (root is 4) is 3 and the height of the right subtree

(root is 7) is 2, | H

–

HR | = 1. Since both subtrees (of 4 and 7) are balanced, the tree is balanced.

In the left subtree (root is 4), it is balanced because the height of its subtree differs by only 1.

Also since its subtrees (root 2 and 5) are balance, this subtree is a balanced tree. Right subtree

(root 7) is balanced, because the height of its subtree differs by only 1. Continuing this, we make

tree balance.

Example: Fig 11.22 shows the AVL tree with only one node or two nodes.?

Fig. 11.22. An AVL trees with one or two nodes

11.3.2. Insertion into an AVL Tree

As a binary tree, we can insert a new node x into an AVL tree, keeping tree balanced in any case.

It means that we must insert new node x without changing the height of the subtree. Thus, it is

important that the height (balance) of the root must not be changed. When we insert a new node

x, the height of the root may increase. Thus, we must adjust the balance factor of the root to

keep an AVL condition | H

–

HR | =

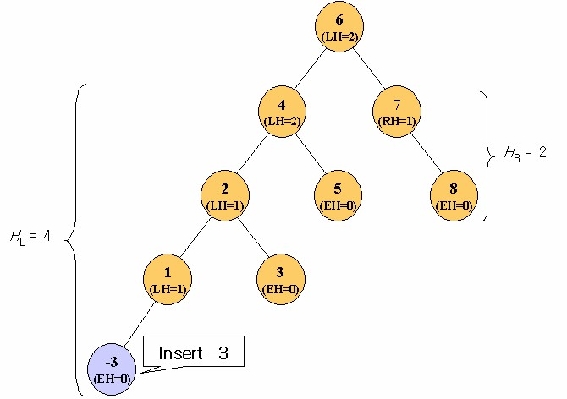
Fig. 11.23 shows a tree to insert new node with -3 into an AVL tree of Fig. 11.21. This tree is not

an AVL tree, because the height of the left subtree is two more than right subtree. Also balance

factors are changed. In order to keep balance of an AVL tree, we must rebuild the tree. This

rebuilding is called rotation.

Rotations

If | H

–

HR | =

2 by inserting a node, we must rebuild the tree to maintain its balance. There

are three considerations to restore balance.

• After a new node is inserted into the AVL tree, if HR – H

2, we rotate the AVL tree to left

to keep the condition | H

–

HR | =

1. By a left rotation, the balance must be restored.

• However, after a new node is inserted into the AVL tree, if H

–

2, we rotate the AVL

tree to right to keep the condition | H

–

HR | =

1. By a right rotation, the balance must be

restored.

• If the insertion makes | H

–

HR | =

1, we do nothing.

Fig. 11.23. A tree with |H

–

HR|=2 after insertion of new node into an AVL tree

From three considerations, we can describe the methods to rebuild the tree to be become an

AVL tree.

Single rotation

This is the case of HR – H

= 2 at root 3 and node 5 of Fig. 11.24 (a). The node 5 is right higher,

since the right height of the node 5 is 3 (HR = 3) and left height of the node 5 is 1 (H

= 1), that is,

–

= 2. Thus, we must rotate the tree to the left to be an AVL tree. It is called the left

rotation. If HR

–

= 2 at two or more nodes in the tree, left rotation is performed with

respect to the closest parent of the new node that a balance factor (RH or LH) was 2.

Fig. 11.24 shows the left rotation in case of HR –

= ², where node 3 is the root of the tree,

and node 5 is the root of its right subtree. Although HR – H

= 2 at both the root 3 and node 5

(pink color), left rotation is performed at the node 5. The action of the left rotation at the node 5

is as follow.

Rotate node 7 upward to the node 5.

Drop node 5 down into the left subtree of node 7.

Link the node 6 to the right subtree of node 5. The key of the node 6 is between key of

node 5 and node 7.

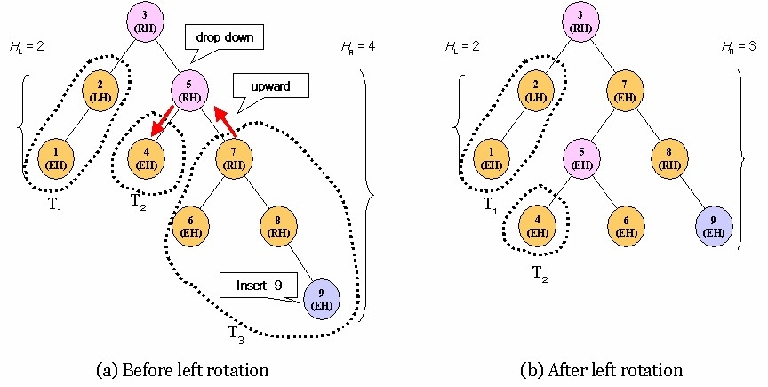
Fig. 11.24. Restoring balance by a left rotation in case of right higher

By the left rotation, although the height has increased by the insertion of a node, the height of

resulting tree decreases by 1. Also the balance factors must be changed appropriately. Following

tables shows change of the balance factors. The circled number in the entry is the balance factor

of the node that the balance is broken at. The first table shows balance factors for Fig. 11.24 (a),

and the second shows balance factors for Fig. 11.24 (b) after left rotation.

Bal. Factor Node No.

Double rotations

This is the case of H

–

2 at node 8 of Fig. 11.25 (a). The node 8 is left higher, since the

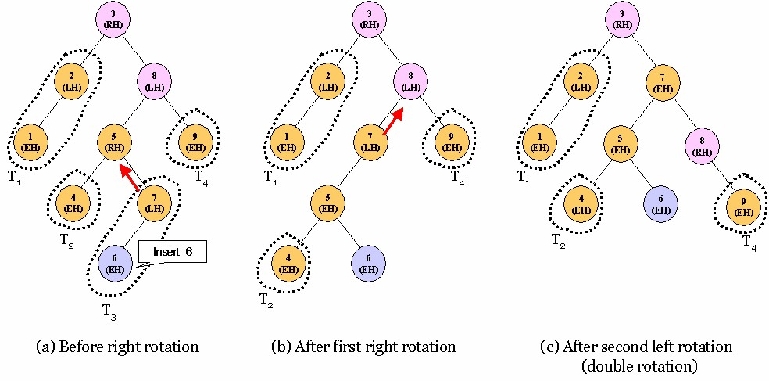
left height of the node 8 is 3 (H

= 3) and right height of the node 8 is 1 (HR= 1), that is, H

–

= 2. Thus, we must rotate the tree to be an AVL tree, but it is complicated.

Since the left subtree of node 8 is left higher, first we have to move node 7 to place of the node 5

as Fig. 11.25 (b). However, since new tree is still right higher (the subtree with root 8 is left

higher), it must rotate to the right to balance as Fig. 11.25 (c). Fig. 11.25 shows that the tree is

balanced by the first left rotation and the second right rotation. It is called double rotation. For

the tree of Fig. 11.25, double rotation performs as follow.

By left rotating the subtree with root 5, node 7 becomes its root.

Link node 7 to the left subtree of node 8.

Link node 5 to the left subtree of node 7, and then link the node 6 to the right subtree of

node 5.

By right rotating the tree with root 8, node 7 becomes new root of the right subtree of the

root 3.

Link node 8 to the right subtree of node 7.

All balance factors for nodes are newly adjusted, depending on the previous balance

factors.

Fig. 11.25. An AVL tree balancing by double rotation in case of left higher

Also the balance factors must be changed appropriately. Following tables is the sequence of

changing the balance factors. The circled number in the entry is the balance factor of the node

that the balance is broken at. The first table shows balance factors for Fig. 11.25 (a), and the

second shows balance factors for Fig. 11.24 (b) after left rotation. Final table shows balance

factors for Fig. 11.25 (c) after right rotation of Fig 11.25 (b).

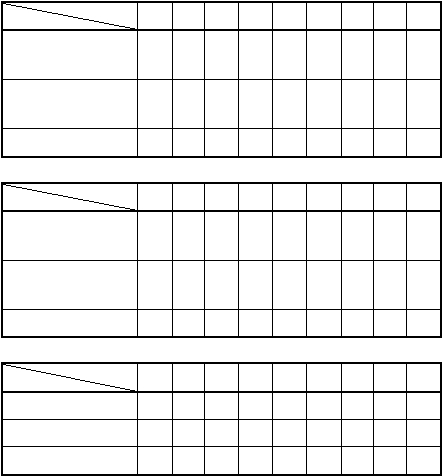
Bal. Factor Node No.